题目内容
有5个同学排队照相,求:
(1)甲、乙2个同学必须相邻的排法有多少种?
(2)甲、乙、丙3个同学互不相邻的排法有多少种?
(1)甲、乙2个同学必须相邻的排法有多少种?
(2)甲、乙、丙3个同学互不相邻的排法有多少种?
考点:计数原理的应用
专题:排列组合
分析:(1)相邻问题,采用捆绑法.先排甲、乙,再与其他3名同学排列,问题得以解决.
(2)不相邻问题,采用插空法,先排其余的2名同学,出现3个空,将甲、乙、丙插空,问题得以解决.
(2)不相邻问题,采用插空法,先排其余的2名同学,出现3个空,将甲、乙、丙插空,问题得以解决.
解答:
解:(1)这是典型的相邻问题,采用捆绑法.先排甲、乙,有
种方法,再与其他3名同学排列,共有
•
=48种不同排法.
(2)这是不相邻问题,采用插空法,先排其余的2名同学,有
种排法,出现3个空,将甲、乙、丙插空,所以共有
•
=12种排法.
| A | 2 2 |
| A | 2 2 |
| A | 4 4 |
(2)这是不相邻问题,采用插空法,先排其余的2名同学,有
| A | 2 2 |
| A | 2 2 |
| A | 3 3 |
点评:本题主要考查了排列中相邻不相邻的问题,相邻用捆绑,不相邻用插空,属于基础题.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
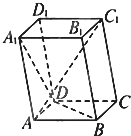 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.