题目内容
已知函数y=x2-2ax+
的两个零点分别在区间（0，1）和（1，2）内，求实数a的取值范围．
| 3 |
| 4 |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：令f（x）=x2-2ax+
，若函数y=x2-2ax+
的两个零点分别在区间（0，1）和（1，2）内，则
，进而可得实数a的取值范围．
| 3 |
| 4 |
| 3 |
| 4 |
|
解答：
解：令y=f（x）=x2-2ax+
，
由y=f（x）=x2-2ax+
的两个零点分别在区间（0，1）和（1，2）内，f（0）=
可得：
，即
解得：a∈（
，
），
故实数a的取值范围为（
，
）
| 3 |
| 4 |
由y=f（x）=x2-2ax+
| 3 |
| 4 |
| 3 |
| 4 |
|
|
解得：a∈（
| 7 |
| 8 |
| 19 |
| 16 |
故实数a的取值范围为（
| 7 |
| 8 |
| 19 |
| 16 |
点评：本题考查的知识点是函数零点的判定定理，将问题转化为
，是解答的关键．
|
练习册系列答案
相关题目
各项均不为0的等差数列{an}中，若an2-an-1-an+1=0（n∈N*，n≥2），Sn为数列的前n项和，则S2012=（ ）
| A、0 | B、2011 |
| C、2012 | D、4024 |
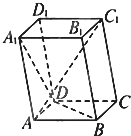已知平行六面体ABCD-A1B1C1D1中，底面ABCD是边长为1的正方形．AA1=2，∠A1AB=∠A1AD=120°．