题目内容
一名学生每天骑自行车上学,从家到学校的途中有5个交通岗,假设他在各交通岗遇到红灯的事件是相互独立的,并且概率都是
.
(1)求这名学生在途中遇到红灯的次数ξ的分布列;
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;
(3)这名学生在途中至少遇到一次红灯的概率.
| 1 |
| 3 |
(1)求这名学生在途中遇到红灯的次数ξ的分布列;
(2)求这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列;
(3)这名学生在途中至少遇到一次红灯的概率.
考点:离散型随机变量及其分布列
专题:概率与统计
分析:(1)由ξ~B(5,
),能求出这名学生在途中遇到红灯的次数ξ的分布列.
(2)η=k(k=0,1,2,3,4),也就是说{前k个是绿灯,第k+1个是红灯},η=5,也就是说(5个均为绿灯),则P(η=k)=(
)k•
,k=0,1,2,3,4,由此能求出这名学生在首次遇到红灯或到达目的地停车前经过的路口数η的分布列.
(3)利用对立事件概率计算公式能求出这名学生在途中至少遇到一次红灯的概率.
| 1 |
| 3 |
(2)η=k(k=0,1,2,3,4),也就是说{前k个是绿灯,第k+1个是红灯},η=5,也就是说(5个均为绿灯),则P(η=k)=(
| 2 |
| 3 |
| 1 |
| 3 |
(3)利用对立事件概率计算公式能求出这名学生在途中至少遇到一次红灯的概率.
解答:
解:(1)由于ξ~B(5,
),
则P(ξ=k)=
(
)k(
)5-k,k=0,1,2,3,4,5;
所以ξ的分布列为:
(2)η=k(k=0,1,2,3,4),
也就是说{前k个是绿灯,第k+1个是红灯},η=5,
也就是说(5个均为绿灯),
则P(η=k)=(
)k•
,k=0,1,2,3,4;
P(η=5)=(
)5=
;
所以η的分布列为:
(3)所求概率P(ξ≥1)=1-P(ξ=0)=1-(
)5=
.
| 1 |
| 3 |
则P(ξ=k)=
| C | k 5 |
| 1 |
| 3 |
| 2 |
| 3 |
所以ξ的分布列为:
| ξ | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
也就是说{前k个是绿灯,第k+1个是红灯},η=5,
也就是说(5个均为绿灯),
则P(η=k)=(
| 2 |
| 3 |
| 1 |
| 3 |
P(η=5)=(
| 2 |
| 3 |
| 32 |
| 243 |
所以η的分布列为:
| η | 0 | 1 | 2 | 3 | 4 | 5 | ||||||||||||
| P |
|
|
|
|
|
|
| 2 |
| 3 |
| 211 |
| 243 |
点评:本题考查概率的求法,考查离散型随机变量的分布列的求法,是中档题.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
函数y=log
(x2-ax+3)在[1,2]上恒为正数,则a的取值范围是( )
| 1 |
| 3 |
A、2
| ||||
B、2
| ||||
C、3<a<
| ||||
D、3<a<2
|
各项均不为0的等差数列{an}中,若an2-an-1-an+1=0(n∈N*,n≥2),Sn为数列的前n项和,则S2012=( )
| A、0 | B、2011 |
| C、2012 | D、4024 |

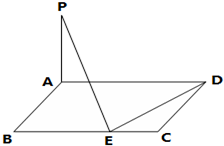 (理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.
(理)如图,已知矩形ABCD中,AB=3,BC=a,若PA⊥平面ABCD,在BC边上取点E,使得PE⊥DE,则满足条件的E点有两个时,求实数a的取值范围.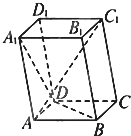 已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.
已知平行六面体ABCD-A1B1C1D1中,底面ABCD是边长为1的正方形.AA1=2,∠A1AB=∠A1AD=120°.