如图所示.在三棱锥S-ABC中.SA⊥SB.SB⊥SC.SA⊥SC.且SA.SB.SC和底面ABC所成的角分别为a1.a2.a3.三侧面△SBC.△SAC.△SAB的面积分别为S1.S2.S3.类比三角形中的正弦定理.给出空间情形的一个猜想．题目和参考答案——青夏教育精英家教网—

题目内容

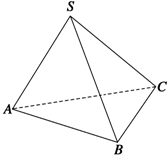如图所示，在三棱锥S-ABC中，SA⊥SB，SB⊥SC，SA⊥SC，且SA、SB、SC和底面ABC所成的角分别为a₁、a₂、a₃，三侧面△SBC、△SAC、△SAB的面积分别为S₁、S₂、S₃，类比三角形中的正弦定理，给出空间情形的一个猜想．

考点：类比推理

专题：常规题型,推理和证明

分析：由类比推理猜想结论，结论不一定正确．

解答： 解　解　在△DEF中，由正弦定理，

得

sinD

sinE

sinF

．
于是，类比三角形中的正弦定理，
在四面体S-ABC中，
我们猜想

sinα1

sinα2

sinα3

成立．

点评：本题考查了类比推理．属于基础题．

练习册系列答案

相关题目

某城市连锁经营公司所属的5个零售店某月的销售额和利润额资料如下表：

商店名称	A	B	C	D	E
销售额（x）/千万元	3	5	6	7	9
利润额（y）/百万元	2	3	3	4	5

（1）画出销售额和利润额的散点图，并判断销售额和利润额是否具有相关关系；
（2）求利润额y对销售额x的回归直线方程．
（参考：b=

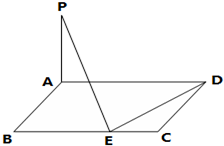（理）如图，已知矩形ABCD中，AB=3，BC=a，若PA⊥平面ABCD，在BC边上取点E，使得PE⊥DE，则满足条件的E点有两个时，求实数a的取值范围．

为了对某课题进行研究，用分层抽样方法从三所高校A，B，C的相关人员中，抽取若干人组成研究小组、有关数据见下表（单位：人）

高校	相关人数	抽取人数
A	18	x
B	36	2
C	54	y

（Ⅰ）求x，y；
（Ⅱ）若从高校A、C抽取的人中选2人作专题发言，求这二人是高校A、C各一人的概率．

．
（1）设A是△ABC的内角，且为钝角，求f（A）的最小值；
（2）设A，B是锐角△ABC的内角，且A+B=

7π

，f（A）=1，BC=2，求△ABC 的三个内角的大小和AC边的长．

已知动点M到点A（2，0）的距离是它到点B（8，0）的距离的一半；直线l的方程为y-1=k（x+1）．
（1）求M的轨迹方程；
（2）判断l与M的轨迹的位置关系，若相交求出最短的弦长；
（3）设l与M的轨迹相交于A、B两点，是否存在k使得OA⊥OB？若存在求出k；若不存在，请给予证明．

已知圆x²+y²-6mx-2（m-1）y+10m²-2m-24=0．m∈R．求证：
（1）不论m取何值，圆心在同一条直线l上；
（2）与l平行的直线被圆所截得的线段长与m无关．

已知函数f（x）是定义在R上的偶函数，且当x≥0时，f（x）=x²+2x．
（1）写出函数f（x）在x∈R的解析式；
（2）若函数g（x）=f（x）-2ax+2（x∈[1，2]），求函数g（x）的最小值．

试题分类