题目内容
对任意实数x,[x]表示不超过x的最大整数,如[3.6]=3,[-3.6]=-4,关于函数f(x)=[
-[
]],有下列命题:
①f(x)是周期函数;
②f(x)是偶函数;
③函数f(x)的值域为{0,1};
④函数g(x)=f(x)-cosπx在区间(0,π)内有两个不同的零点,
其中正确的命题为 (把正确答案的序号填在横线上).
| x+1 |
| 3 |
| x |
| 3 |
①f(x)是周期函数;
②f(x)是偶函数;
③函数f(x)的值域为{0,1};
④函数g(x)=f(x)-cosπx在区间(0,π)内有两个不同的零点,
其中正确的命题为
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:根据函数f(x)的表达式,结合函数的周期性,奇偶性和值域分别进行判断即可得到结论.
解答:
解:∵f(x+3)=[
-[
]]=[
+1-[
+1]]=f(x),∴f(x)是周期函数,3是它的一个周期,故①正确.
f(x)=[
-[
]]=
,结合函数的周期性可得函数的值域为{0,1},则函数不是偶函数,故②错,③正确.
f(x)=[
-[
]]=
,故g(x)=f(x)-cosπx在区间(0,π)内有3个不同的零点
,
,2,故④错误.
则正确的命题是①③,
故答案为:①③
| x+4 |
| 3 |
| x+3 |
| 3 |
| x+1 |
| 3 |
| x |
| 3 |
f(x)=[
| x+1 |
| 3 |
| x |
| 3 |
|
f(x)=[
| x+1 |
| 3 |
| x |
| 3 |
|
| 1 |
| 2 |
| 3 |
| 2 |
则正确的命题是①③,
故答案为:①③
点评:本题主要考查与函数性质有关的命题的真假判断,正确理解函数f(x)的意义是解决本题的关键.综合性较强,难度较大.

练习册系列答案
相关题目
 设函数y=
设函数y=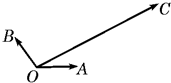 如图平面内有三个向量
如图平面内有三个向量