题目内容
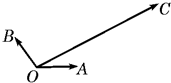 如图平面内有三个向量
如图平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
| OC |
| OA |
| OB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:如图所示,由
与
的夹角为120°,
与
的夹角为30°,|
|=|
|=1,|
|=4
.可得A(1,0),B(-
,
),C(6,2
).代入
=λ
+μ
,利用共面向量基本定理即可得出.
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| OC |
| OA |
| OB |
解答:
解:如图所示,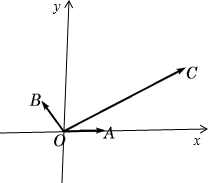
∵
与
的夹角为120°,
与
的夹角为30°,|
|=|
|=1,|
|=4
.
∴A(1,0),B(-
,
),C(6,2
).
∵
=λ
+μ
,
∴(6,2
)=λ(1,0)+μ(-
,
).
∴
,解得
.
∴λ+μ=12.
故答案为:12.

∵
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
∴A(1,0),B(-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
∵
| OC |
| OA |
| OB |
∴(6,2
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴
|
|
∴λ+μ=12.
故答案为:12.
点评:本题考查了向量的坐标运算、共面向量基本定理,考查了计算能力,属于基础题.

练习册系列答案
相关题目
 为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题:
为了让学生了解更多“奥运会”知识,某中学举行了一次“奥运知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表,解答下列问题: