题目内容
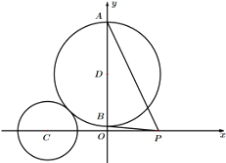 已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)
已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)(Ⅰ)圆D的圆心在什么位置时,圆D与x轴相切;
(Ⅱ)在x轴正半轴上求点P,当圆心D在y轴的任意位置时,直线AP与直线BP的夹角为定值,并求此常数.
考点:直线和圆的方程的应用
专题:综合题,直线与圆
分析:(I)设D(0,a),则由题意可得
=2+|a|,解方程,可得a的值,从而可得D的坐标.
(Ⅱ)假设存在点P(x,0),根据直线AP与直线BP的夹角为定值,我们构造关于x的方程,若方程有解,则存在这样的点,若方程无实根,则不存在这样的点.
| 42+a2 |
(Ⅱ)假设存在点P(x,0),根据直线AP与直线BP的夹角为定值,我们构造关于x的方程,若方程有解,则存在这样的点,若方程无实根,则不存在这样的点.
解答:
解:(I)设D(0,a),则
∵圆D与x轴相切,∴圆D半径r=|a|.
又∵圆D与圆C外切,∴
=2+|a|,
∴16+a2=4+4|a|+a2,
∴|a|=3,即a=±3.
∴当D在(0,3)或(0,-3)时,圆D与x轴相切;
(Ⅱ)证明:假设存在点P(x,0),x>0,圆D的方程为x2+(y-a)2=r2.
当D在y轴上运动时,令D(0,t),|CD|=
,
圆D的半径R=
-2,A(0,t+R),B(0,t-R),
∵∠APB=∠APC-∠BPC,
∴tan∠APB=
=
为常数
∴
=
,
∵x>0,
∴x=2
,
∴存在满足题意的点P的坐标为(2
,0),直线AP与直线BP的夹角为
.
∵圆D与x轴相切,∴圆D半径r=|a|.
又∵圆D与圆C外切,∴
| 42+a2 |
∴16+a2=4+4|a|+a2,
∴|a|=3,即a=±3.
∴当D在(0,3)或(0,-3)时,圆D与x轴相切;
(Ⅱ)证明:假设存在点P(x,0),x>0,圆D的方程为x2+(y-a)2=r2.
当D在y轴上运动时,令D(0,t),|CD|=
| t2+16 |
圆D的半径R=
| t2+16 |
∵∠APB=∠APC-∠BPC,
∴tan∠APB=
| 2rx |
| x2+t2-r2 |
2x
| ||
4
|
∴
| 2x |
| 4 |
| -4x |
| x2-20 |
∵x>0,
∴x=2
| 3 |
∴存在满足题意的点P的坐标为(2
| 3 |
| π |
| 3 |
点评:本题重点考查直线和圆的方程的应用,考查直线的倾斜角与斜率,考查存在性问题,有综合性.

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
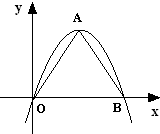 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.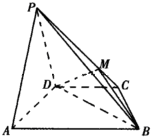 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,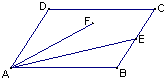 如图,平行四边形ABCD中,AB=3,BC=2,
如图,平行四边形ABCD中,AB=3,BC=2, 如图,已知线段AB、BD在平面α内,BD⊥AB,线段AC⊥α,如果AB=2,BD=5,AC=4,则C、D间的距离为
如图,已知线段AB、BD在平面α内,BD⊥AB,线段AC⊥α,如果AB=2,BD=5,AC=4,则C、D间的距离为