题目内容

已知sinα=
5
5
，且α是第一象限角．
（1）求cosα的值；
（2）求tan(α+π)+
sin(
3π
2
-α)
cos(π-α)
的值．
考点：同角三角函数基本关系的运用,运用诱导公式化简求值
专题：三角函数的求值
分析：（1）由α是第一象限角，得到cosα大于0，根据sinα的值，利用同角三角函数间的基本关系求出cosα的值即可；
（2）由sinα与cosα的值，求出tanα的值，原式利用诱导公式化简后，将tanα的值代入计算即可求出值．
解答： 解：（1）∵α是第一象限角，
∴cosα＞0，
∵sinα=
5
5
，
∴cosα=
1-sin2α
=
2
5
5
；
（2）∵tanα=
sinα
cosα
=
1
2
，
∴原式=tanα+
-cosα
-cosα
=tanα+1=
3
2
．
点评：此题考查了同角三角函数基本关系的运用，以及运用诱导公式化简求值，熟练掌握诱导公式及基本关系是解本题的关键．
练习册系列答案
相关题目
已知曲线y=Asin（wx+φ）（A＞0，w＞0）上的一个最高点的坐标为（
π
2
，
2
），由此点到相邻最低点间的曲线与x轴交于点（
3
2
π，0），φ∈（-
π
2
，
π
2
）．
（1）求这条曲线的函数解析式；
（2）求函数的单调增区间．
设函数f（x）=
1
x2-1
，
（1）求函数f（x）的定义域、值域；
（2）判断函数f（x）的奇偶性；
（3）指出函数f（x）的单调区间并就其中一种情况加以证明．
已知函数f（x）=sin（ωx+φ） (ω＞0，0＜φ＜
2π
3
)的最小正周期为π，
（1）求当f（x）为偶函数时φ的值；
（2）若f（x）的图象过点（
π
6
，
3
2
），求f（x）的单调递增区间．
如图所示，在长方体ABCD-A1B1C1D1中，AA1=2，AB=AD=1，点M是CC1的中点，
①求证：平面ABM⊥平面A1B1M；
②求直线BD与平面ABM所成角的大小．
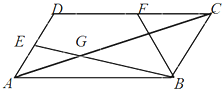如图所示，在平行四边形ABCD中，∠BAD=
π
3
，AB=2，AD=1，点E、F分别是边AD、DC上的动点，且
|
CF|
|
CD|
=
|
DE|
|
DA|
=t，BE与AC交于G点．
（1）若t=
1
2
，试用向量
AB
，
AD
表示向量
AG
；
（2）求
BG
•
BF
的取值范围．
已知集合M={x|2x2-（2a+1）x+a＞0，a＞
1
2
}，集合N={x|?t∈R，使得t2+t+1≤x成立}，若x∈N是x∈M的充分不必要条件，求实数a的取值范围．
已知角α的终边经过点P（-3，4），求角α的正弦、余弦、正切函数值．
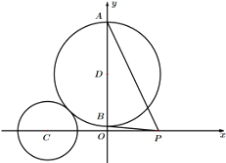已知圆C：（x+4）2+y2=4，圆D的圆心在y轴上且与圆C外切，圆D与y轴交于A、B两点（点A在点B上方）
（Ⅰ）圆D的圆心在什么位置时，圆D与x轴相切；
（Ⅱ）在x轴正半轴上求点P，当圆心D在y轴的任意位置时，直线AP与直线BP的夹角为定值，并求此常数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网