题目内容
在△ABC中,
=(cos18°,cos72°),
=(2cos63°,2cos27°),则∠B= .
| AB |
| BC |
考点:平面向量数量积的坐标表示、模、夹角,三角函数中的恒等变换应用
专题:平面向量及应用
分析:利用向量的夹角公式和数量积运算、模的计算公式、三角函数的平方关系、两角和差的正弦公式即可得出.
解答:
解:∵
•
=-cos18°•2cos63°-cos72°•2cos27°
=-2(sin27°cos18°+cos27°sin18°)=-2sin45°=-
.
|
|=
=
=1,|
|=
=2
=2.
∴cosB=
=
,
∴∠B=135°.
故答案为:135°.
| BA |
| BC |
=-2(sin27°cos18°+cos27°sin18°)=-2sin45°=-
| 2 |
|
| BA |
| cos218°+cos272° |
| cos218°+sin218° |
| BC |
| 4cos263°+4cos227° |
| sin227°+cos227° |
∴cosB=
| ||||
|
|
-
| ||
| 2 |
∴∠B=135°.
故答案为:135°.
点评:本题考查了向量的夹角公式和数量积运算、模的计算公式、三角函数的平方关系、诱导公式、两角和差的正弦公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
某车间分批生产某种产品,每批的生产准备费用为400元,若每批生产x件,则平均仓储时间为
天,且每件产品每天的仓储费用为2元,为使平均到每件产品的生产准备费用与仓储费用之和最小,则每批应生产产品为 .
| x |
| 8 |
已知函数f(x)=
•
,则函数的定义域为( )
| x-2 |
| x+5 |
| A、{x|x≥-2} |
| B、{x|x≥-5} |
| C、{x|x≤5} |
| D、{x|x≥2} |
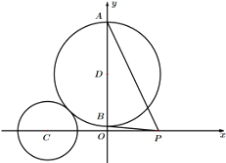 已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)
已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)