题目内容
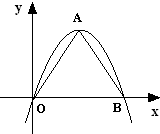 如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.
如果一条抛物线y=ax2+bx+c(a≠0)与x轴有两个交点,那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条抛物线的“抛物线三角形”.(Ⅰ)“抛物线三角形”一定是
(Ⅱ)若抛物线m:y=a(x-2)2+b(a>0,b<0)的“抛物线三角形”是直角三角形,求a,b满足的关系式;
(Ⅲ)如图,△OAB是抛物线n:y=-x2+tx(t>0)的“抛物线三角形”,是
否存在以原点O为对称中心的矩形ABCD?若存在,求出过O、C、D三点的抛物线的表达式;若不存在,说明理由.
考点:直线与圆锥曲线的关系
专题:压轴题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)“根据抛物线的对称性进行判断;
(Ⅱ)由于抛物线三角形是等腰三角形,则得到本题中的“物线三角形”是等腰直角三角形,再确定抛物线的顶点坐标为(2,b),抛物线与x轴两交点之间的线段长=2
,如何根据等腰直角三角形的性质得到|b|=
×2
,然后化简即可得到a与b的关系;
(Ⅲ)作分别作点A,B关于原点O的对称点C,D,所以四边形ABCD是平行四边形,确定A、B两点坐标,然后根据关于原点中心的性质可确定C点与D点坐标,最后利用待定系数法求抛物线的解析式.
(Ⅱ)由于抛物线三角形是等腰三角形,则得到本题中的“物线三角形”是等腰直角三角形,再确定抛物线的顶点坐标为(2,b),抛物线与x轴两交点之间的线段长=2
-
|
| 1 |
| 2 |
-
|
(Ⅲ)作分别作点A,B关于原点O的对称点C,D,所以四边形ABCD是平行四边形,确定A、B两点坐标,然后根据关于原点中心的性质可确定C点与D点坐标,最后利用待定系数法求抛物线的解析式.
解答:
解:(I))因为抛物线与x轴有两个交点关于抛物线的对称轴对称,
所以“抛物线三角形”是等腰三角形;
故答案为等腰; …(2分)
(II)设抛物线线与x轴的交点为A,B,当y=a(x-2)2+b=0时,得x=2±
所以A(2-
),B(2+
),AB=2
,…(4分)
又因为抛物线顶点P(2,b)由已知三角形PAB是等腰直角三角形,所以AB=2|yp|,
所以2
=2|b|,整理得ab=-1…(6分)
(3)分别作点A,B关于原点O的对称点C,D,所以四边形ABCD是平行四边形,
所以当OA=OB时,四边形ABCD是矩形,三角形OAB是等边三角形y=-x2+tx=-(x-
)2+
,
所以A点坐标是(
,
),
又点B坐标是(t,0),yA=
|OB|,
=
t,t=2
,…(8分)
所以A(
,3),B(2
,0),
所以C(-
,-3),D(-2
,0)
设过O、C、D三点的抛物线为y=mx(x+2
),
因为过点C,所以-3=m(-
)(-
+2
),m=1
所以存在以原点O为对称中心的矩形ABCD
所求抛物线的表达式为y=x2+2
x. …(10分)
所以“抛物线三角形”是等腰三角形;
故答案为等腰; …(2分)
(II)设抛物线线与x轴的交点为A,B,当y=a(x-2)2+b=0时,得x=2±
-
|
所以A(2-
-
|
-
|
-
|
又因为抛物线顶点P(2,b)由已知三角形PAB是等腰直角三角形,所以AB=2|yp|,
所以2
-
|
(3)分别作点A,B关于原点O的对称点C,D,所以四边形ABCD是平行四边形,
所以当OA=OB时,四边形ABCD是矩形,三角形OAB是等边三角形y=-x2+tx=-(x-
| t |
| 2 |
| t2 |
| 4 |
所以A点坐标是(
| t |
| 2 |
| t2 |
| 4 |
又点B坐标是(t,0),yA=
| ||
| 2 |
| t2 |
| 4 |
| ||
| 2 |
| 3 |
所以A(
| 3 |
| 3 |
所以C(-
| 3 |
| 3 |
设过O、C、D三点的抛物线为y=mx(x+2
| 3 |
因为过点C,所以-3=m(-
| 3 |
| 3 |
| 3 |
所以存在以原点O为对称中心的矩形ABCD
所求抛物线的表达式为y=x2+2
| 3 |
点评:本题考查了抛物线的综合题:熟练掌握二次函数的性质,并且根据二次函数的性质确定几何图形的性质和确定点的坐标;会运用等腰直角三角形、等边三角形和矩形的性质建立等量关系,将函数问题转化为方程问题.

练习册系列答案
相关题目
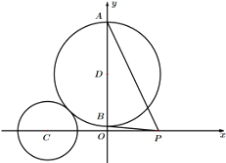 已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)
已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)