题目内容
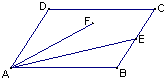 如图,平行四边形ABCD中,AB=3,BC=2,
如图,平行四边形ABCD中,AB=3,BC=2,| AD |
| AB |
| 1 |
| 3 |
| AB |
(Ⅰ)求∠BAD的大小;
(Ⅱ)若E为BC边上的中点,F为平行四边形内(包括边界)的一动点,求
| AE |
| AF |
考点:向量在几何中的应用
专题:计算题,平面向量及应用
分析:(Ⅰ)根据向量数量积的定义,结合题中数据算出cos∠BAD=
,从而可得∠BAD的大小;
(Ⅱ)作出如图所求直角坐标系,算出E、C两点的坐标,设F(x,y),利用向量数量积的坐标运算,可得当x=4且y=
时,
•
的最大值为
.
| 1 |
| 2 |
(Ⅱ)作出如图所求直角坐标系,算出E、C两点的坐标,设F(x,y),利用向量数量积的坐标运算,可得当x=4且y=
| 3 |
| AE |
| AF |
| 31 |
| 2 |
解答:
解:(Ⅰ)∵
•
=
|
|2,
∴
•
cos∠BAD=
×32=3,即2×3×cos∠BAD=3,
解得cos∠BAD=
结合∠BAD∈[0,π],可得∠BAD=
;
(Ⅱ)以AB所在直线为x轴,A为原点建立如图所示直角坐标系,
则E(
,
),C(4,
)
设F(x,y),根据题意可得x≤4,y≤
∴
•
=
x+
y≤
×4+
×
=
.
即
•
的最大值等于
.
| AD |
| AB |
| 1 |
| 3 |
| AB |
∴
| |AD| |
| |AB| |
| 1 |
| 3 |

解得cos∠BAD=
| 1 |
| 2 |
结合∠BAD∈[0,π],可得∠BAD=
| π |
| 3 |
(Ⅱ)以AB所在直线为x轴,A为原点建立如图所示直角坐标系,
则E(
| 7 |
| 2 |
| ||
| 2 |
| 3 |
设F(x,y),根据题意可得x≤4,y≤
| 3 |
∴
| AE |
| AF |
| 7 |
| 2 |
| ||
| 2 |
| 7 |
| 2 |
| ||
| 2 |
| 3 |
| 31 |
| 2 |
即
| AE |
| AF |
| 31 |
| 2 |
点评:本题给出平行四边形中的向量满足的条件,求∠BAD的大小,并依此求向量数量积的最值.着重考查了平面向量数量积的定义、运算运算法则等知识,属于中档题.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案
相关题目
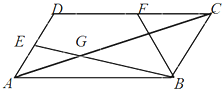 如图所示,在平行四边形ABCD中,∠BAD=
如图所示,在平行四边形ABCD中,∠BAD=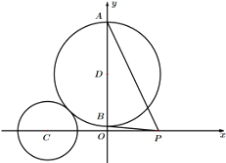 已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)
已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)