题目内容
已知点P（a，0），对于抛物线y2=2x上任一点Q，都有|PQ|≥|a|，则实数a的取值范围 ．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：设Q（x，y），由P（a，0），利用两点间的距离公式能求出|PQ|2=（x+1-a）2+（2a-1），（x≥0），再由二次函数的性质能求出实数a的取值范围．
解答：
解：设Q（x，y），
∵P（a，0），
∴|PQ|2=（x-a）2+y2
=（x-a）2+2x
=x2+2（1-a）x+a2
=（x+1-a）2+（2a-1），（x≥0）
这是个二次函数，对称轴x=a-1，
若a-1≥0，a≥1，则当x=a-1时，|QP|min=
．
若a-1＜0，a＜1，则当x=0时，|QP|min=|a|．
∴当a＜1时，有|PQ|≥|a|．
由
≥|a|，解得：a=1．
综上，实数a的取值范围是（-∞，1]．
故答案为：（-∞，1]．
∵P（a，0），
∴|PQ|2=（x-a）2+y2
=（x-a）2+2x
=x2+2（1-a）x+a2
=（x+1-a）2+（2a-1），（x≥0）
这是个二次函数，对称轴x=a-1，
若a-1≥0，a≥1，则当x=a-1时，|QP|min=
| 2a-1 |
若a-1＜0，a＜1，则当x=0时，|QP|min=|a|．
∴当a＜1时，有|PQ|≥|a|．
由
| 2a-1 |
综上，实数a的取值范围是（-∞，1]．
故答案为：（-∞，1]．
点评：本题考查满足条件的实数的取值范围的求法，是中档题，解题时要注意两点间距离公式和二次函数性质的灵活运用．
练习册系列答案
相关题目
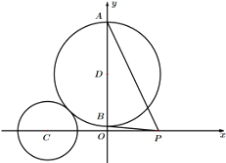已知圆C：（x+4）2+y2=4，圆D的圆心在y轴上且与圆C外切，圆D与y轴交于A、B两点（点A在点B上方）