题目内容
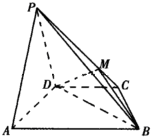 在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,AB=2DC=4
在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB∥CD,在锐角△PAD中PA=PD,并且BD=2AD=8,AB=2DC=4| 5 |
(1)点M是PC上的一点,证明:平面MBD⊥平面PAD;
(2)若PA与平面PBD成角60°,当面MBD⊥平面ABCD时,求点M到平面ABCD的距离.
考点:点、线、面间的距离计算,平面与平面垂直的判定
专题:计算题,证明题,空间位置关系与距离
分析:法一:(1)通过证明平面MBD内的直线BD,垂直平面PAD内的两条相交直线,证明直线与平面垂直然后证明两个平面垂直.
(2)PA与平面PBD成角60°,面MBD⊥平面ABCD时,做PF⊥AD于F,PF∥MN,然后求点M到平面ABCD的距离.
法二:(1)同法一;
(2)建立空间直角坐标系,求出平面的法向量,利用点到平面的距离公式求解即可.
(2)PA与平面PBD成角60°,面MBD⊥平面ABCD时,做PF⊥AD于F,PF∥MN,然后求点M到平面ABCD的距离.
法二:(1)同法一;
(2)建立空间直角坐标系,求出平面的法向量,利用点到平面的距离公式求解即可.
解答:
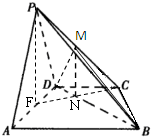 解:法一(1)∵BD=2AD=8,AB=4
解:法一(1)∵BD=2AD=8,AB=4
,由勾股定理得BD⊥AD,
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD⊆面ABCD,
∴BD⊥平面PADBD⊆面MBD,
∴平面MBD⊥平面PAD…(6分)
(2)如图,∵BD⊥平面PAD,∴平面PBD⊥平面PAD,∴∠APD=60°,
做PF⊥AD于F,∴PF⊥面ABCD,PF=2
,
设面PFC∩面MBD=MN,面MBD⊥平面ABCD∴面PF∥面MBD,∴PF∥MN,
取DB中点Q,得CDFQ为平行四边形,由平面ABCD边长得N为FC中点,
∴MN=
PF=
…(12分)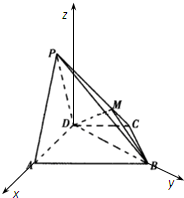
法二(1)同一
(2)在平面PAD过D做AD垂线为z轴,由(1),以D为原点,DA,DB为x,y轴建立空间直角坐标系,
设平面PBD法向量为
=(x,y,z),设P(2,0,a),
锐角△PAD,AD=4
∴a>2,
由
•
=0,
•
=0,
解得
=(-a,0,2),
=(2,0,-a),|cos<
,
>|=
=
,
解得a=2
或a=
<2(舍)
设
=λ
,解得M(2-4λ,4λ,2
-2
λ)
∵面MBD⊥平面ABCD,AD⊥BD,
∴面MBD法向量为
=(0,0,4),∴
•
=0,解得λ=
,
∴M到平面ABD的距离为竖坐标
. …(12分)
 解:法一(1)∵BD=2AD=8,AB=4
解:法一(1)∵BD=2AD=8,AB=4| 5 |
∵平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,BD⊆面ABCD,
∴BD⊥平面PADBD⊆面MBD,
∴平面MBD⊥平面PAD…(6分)
(2)如图,∵BD⊥平面PAD,∴平面PBD⊥平面PAD,∴∠APD=60°,
做PF⊥AD于F,∴PF⊥面ABCD,PF=2
| 3 |
设面PFC∩面MBD=MN,面MBD⊥平面ABCD∴面PF∥面MBD,∴PF∥MN,
取DB中点Q,得CDFQ为平行四边形,由平面ABCD边长得N为FC中点,
∴MN=
| 1 |
| 2 |
| 3 |

法二(1)同一
(2)在平面PAD过D做AD垂线为z轴,由(1),以D为原点,DA,DB为x,y轴建立空间直角坐标系,
设平面PBD法向量为
| u |
锐角△PAD,AD=4
∴a>2,
由
| u |
| DP |
| u |
| DB |
解得
| u |
| PA |
| PA |
| u |
| 4a |
| a2+4 |
| ||
| 2 |
解得a=2
| 3 |
2
| ||
| 3 |
设
| PM |
| PC |
| 3 |
| 3 |
∵面MBD⊥平面ABCD,AD⊥BD,
∴面MBD法向量为
| DA |
| DA |
| DM |
| 1 |
| 2 |
∴M到平面ABD的距离为竖坐标
| 3 |
点评:本题考查两个平面垂直的判断,点到平面的距离的求法,考查空间想象能力以及计算能力.

练习册系列答案
相关题目
 如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,
如图所示,在长方体ABCD-A1B1C1D1中,AA1=2,AB=AD=1,点M是CC1的中点,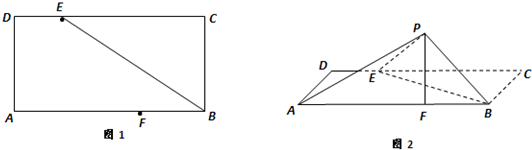
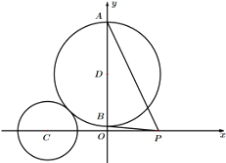 已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)
已知圆C:(x+4)2+y2=4,圆D的圆心在y轴上且与圆C外切,圆D与y轴交于A、B两点(点A在点B上方)