题目内容
16.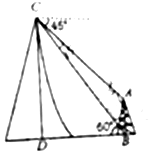 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
分析 设CD=x m,则AE=x-20 m,求出BD,在△AEC中,列出关系式,解得x就是山高CD.
解答 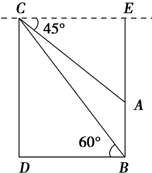 解:如图,设CD=x m,
解:如图,设CD=x m,
则AE=x-20 m,
tan 60°=$\frac{CD}{BD}$,
∴BD=$\frac{CD}{tan60°}$=$\frac{x}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}x$ (m)…(6分)
在△AEC中,x-20=$\frac{\sqrt{3}}{3}$x,
解得x=10(3+$\sqrt{3}$) m.
故山高CD为10(3+$\sqrt{3}$) m…(12分).
故答案为:10(3+$\sqrt{3}$).
点评 本题考查三角形的解法,实际应用,基本知识的考查.

练习册系列答案
相关题目
4.下列函数中,既是偶函数又在(0,π)上单调递增的是( )
| A. | y=tanx | B. | y=cos(-x) | C. | $y=-sin({\frac{π}{2}-x})$ | D. | y=|tanx| |
6.若z∈C,且|z|=1,则|z-i|的最大值为( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
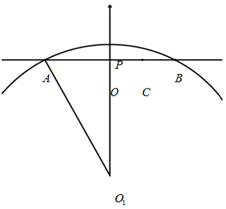 如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).