题目内容
1.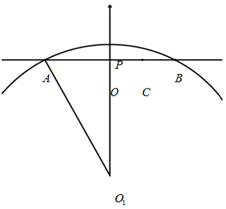 如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
分析 建立平面直角坐标系,利用勾股定理求出圆的半径,写出圆的方程,利用圆的方程求直立柱的高度即可.
解答  解:如图建立平面直角坐标系,
解:如图建立平面直角坐标系,
设圆的半径为r,
在Rt△O1OA中:OA=20,OO1=r-5,O1A=r;
∴r2=202+(r-5)2,
解得r=42.5;
∴圆的方程为x2+(y+37.5)2=42.52;
令x=10,求得y=3.81(米),
即所求直立柱的高度为3.81米.
点评 本题考查了直线与圆的方程应用问题,解题的关键是建立适当的直角坐标系,是基础题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
13.已知倾斜角为α的直线l与直线x-2y+2=0平行,则sinα的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $-\frac{1}{2}$ |
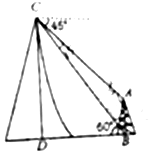 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.