题目内容
8.函数$y=2cos(\frac{π}{5}+3x)$的最小正周期为$\frac{2π}{3}$.分析 利用y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,得出结论.
解答 解:函数$y=2cos(\frac{π}{5}+3x)$的最小正周期为$\frac{2π}{3}$,
故答案为:$\frac{2π}{3}$.
点评 本题主要考查三角函数的周期性及其求法,利用了y=Asin(ωx+φ)的周期等于 T=$\frac{2π}{ω}$,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
13.已知倾斜角为α的直线l与直线x-2y+2=0平行,则sinα的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{5}}}{5}$ | C. | $-\frac{{\sqrt{5}}}{5}$ | D. | $-\frac{1}{2}$ |
18.已知不等式组$\left\{\begin{array}{l}0≤x≤π\\ y≤sinx+a\\ y≥0\end{array}\right.$所对应的平面区域面积为2+2π,则$\sqrt{3}x+2y+1$的最大值为( )
| A. | $\frac{{5\sqrt{3}π}}{6}+6$ | B. | $\sqrt{3}π+7$ | C. | 6 | D. | 7 |
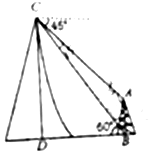 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米. 为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).
为了解某地高中生的身高情况,研究小组在该地高中生中随机抽出30名高中生的身高统计成如图所示的茎叶图(单位:cm).