题目内容
6．已知随机变量ξ服从正态分布N（1，σ2），若P（ξ＞2）=0.15，则P（0≤ξ≤1）=0.35．分析 根据正态分布的对称性计算．
解答 解：∵变量ξ服从正态分布N（1，σ2），
∴P（ξ＞1）=0.5，
∴P（1≤ξ≤2）=P（ξ＞1）-P（ξ＞2）=0.35，
∴P（0≤ξ≤1）=P（1≤ξ≤2）=0.35．
故答案为：0.35．
点评 本题考查了正态分布的特点，属于基础题．
练习册系列答案
相关题目
17．定义运算：$|\begin{array}{l}{{a}_{1}}&{{a}_{2}}\\{{a}_{3}}&{{a}_{4}}\end{array}|$=a1a4-a2a3，将函数f（x）=$|\begin{array}{l}{\sqrt{3}}&{sinωx}\\{1}&{cosωx}\end{array}|$（ω＞0）的图象向左平移$\frac{2π}{3}$个单位，所得图象对应的函数为偶函数，则ω的最小值是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{5}{4}$ | C． | $\frac{7}{4}$ | D． | $\frac{3}{4}$ |
1．已知双曲线x2+$\frac{y^2}{{{b^2}-4}}$=1的焦点到渐近线的距离为2，则双曲线的渐近线方程为（ ）
| A． | y=±$\frac{1}{2}$x | B． | y=±$\sqrt{3}$x | C． | y=±2x | D． | y=±$\frac{{\sqrt{3}}}{3}$x |
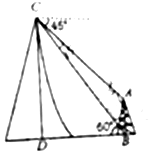如图所示，在塔底B测得山顶C的仰角为60°，在山顶测得塔顶A的仰角为45°，已知塔高AB=20米，则山高DC=10（3+$\sqrt{3}$）米．