题目内容
6.若z∈C,且|z|=1,则|z-i|的最大值为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 由题意画出图形,再由|z-i|的几何意义,即圆上的动点到定点(0,1)的距离求解.
解答 解:由题意,复数z在复平面内对应点的轨迹是以原点为圆心,以1为半径的圆,
|z-i|的几何意义为圆上的动点到定点(0,1)的距离,最大值为2.
故选:B.
点评 本题考查复数的代数表示法及其几何意义,考查复数模的求法,是基础题.

练习册系列答案
相关题目
18.已知不等式组$\left\{\begin{array}{l}0≤x≤π\\ y≤sinx+a\\ y≥0\end{array}\right.$所对应的平面区域面积为2+2π,则$\sqrt{3}x+2y+1$的最大值为( )
| A. | $\frac{{5\sqrt{3}π}}{6}+6$ | B. | $\sqrt{3}π+7$ | C. | 6 | D. | 7 |
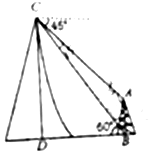 如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米.
如图所示,在塔底B测得山顶C的仰角为60°,在山顶测得塔顶A的仰角为45°,已知塔高AB=20米,则山高DC=10(3+$\sqrt{3}$)米. 四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD
四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD