题目内容
4．某公司从1999年的年产值100万元，增加到10年后2009年的500万元，如果每年产值增长率相同，则每年的平均增长率是多少？（ln（1+x）≈x，lg2=0.3，ln10=2.30）分析 设每年的年产值增长率是x，由题意可得：100（1+x）10=500，化为10ln（1+x）=ln5，即可得出40x=ln5，解出即可得出
解答 解：设每年的年产值增长率是x，
由题意可得：100（1+x）10=500，
化为10ln（1+x）=ln5，
∴10x≈ln5，
∴x=$\frac{ln5}{10}$=$\frac{ln10-ln2}{10}$≈0.2=20%．
答：每年的年产值增长率约是20%
点评 本题属于求增长率（下降率）的模型题，应明确增长的基数，增长的次数．
练习册系列答案
名校练考卷期末冲刺卷系列答案
相关题目
12．如果$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$是二元一次方程组$\left\{\begin{array}{l}{ax+by=1}\\{bx+ay=2}\end{array}\right.$的解，那么a，b的值是（ ）
| A． | $\left\{\begin{array}{l}{a=-1}\\{b=0}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{a=1}\\{b=0}\end{array}\right.$ | C． | $\left\{\begin{array}{l}{a=0}\\{b=1}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{a=0}\\{b=-1}\end{array}\right.$ |
19．已知R上的可导函数f（x）的图象如图所示，则不等式（x2-2x-3）f′（x）＞0的解集为（ ）
| A． | （-∞，-2）∪（1，+∞） | B． | （-∞，-2）∪（1，2） | C． | （-∞，-1）∪（-1，1）∪（3，+∞） | D． | （-∞，-1）∪（-1，0）∪（2，+∞） |
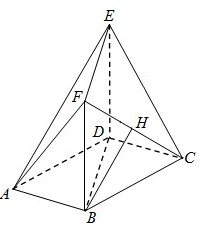如图，在多面体ABCDEF中，底面ABCD是边长为2的菱形，∠BAD=60°，四边形BDEF是矩形，平面BDEF⊥平面ABCD，BF=3，H是CF的中点．
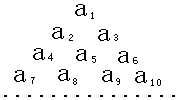已知数列{an}是首项为1，公差为2的等差数列，将数列{an}中的各项排成如图所示的一个三角形数表，记A（i，j）表示第i行从左至右的第j个数，例如A（4，3）=a9，则A（10，2）=93．
13．已知函数f（x）=e2-x+x，x∈[1，3]，则下列说法正确的是（ ）
| A． | 函数f（x）的最大值为$3+\frac{1}{e}$ | B． | 函数f（x）的最小值为$3+\frac{1}{e}$ | ||
| C． | 函数f（x）的最大值为3 | D． | 函数f（x）的最小值为3 |