题目内容
16．
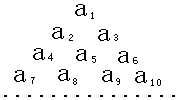已知数列{an}是首项为1，公差为2的等差数列，将数列{an}中的各项排成如图所示的一个三角形数表，记A（i，j）表示第i行从左至右的第j个数，例如A（4，3）=a9，则A（10，2）=93．
分析 观察发现：数阵由连续的项的排列构成，且第m行有m个数，根据等差数列求和公式，得出A（10，6）是数阵中第几个数字，即时数列{an}中的相序，再利用通项公式求出．
解答 解：由数阵可知，S（10，2）是数阵当中第1+2+3+…+9+2=47个数据，
也是数列{an}中的第47项，
而a47=2×47-1=93，
所以S（10，2）对应于数阵中的数是93，
故答案为：93．
点评 本题是规律探究型题目，此题要发现各行的数字个数和行数的关系，从而进行分析计算．
练习册系列答案
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
相关题目
6．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$），$\overrightarrow{b}$=（$\sqrt{3}$，1），则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为（ ）
| A． | 30° | B． | 45° | C． | 60° | D． | 90° |
7．已知a＞0，b＞0，若不等式$\frac{mab}{3a+b}≤a+3b$恒成立，则m的最大值为（ ）
| A． | 4 | B． | 4 | C． | 12 | D． | 16 |
11．已知直线y=3-x与两坐标轴围成的区域为Ω1，不等式组$\left\{\begin{array}{l}y≤3-x\\ x≥0\\ y≥2x\end{array}\right.$所形成的区域为Ω2，现在区域Ω1中随机放置一点，则该点落在区域Ω2的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{2}{3}$ |
1．在正方体ABCD-A1B1C1D1中，M和N分别为A1B1和B1C1的中点，那么直线AM与CN所成角的余弦值是 （ ）
| A． | $\frac{{\sqrt{3}}}{2}$ | B． | $\frac{{\sqrt{10}}}{10}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |