题目内容
9.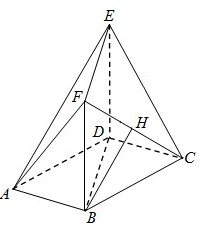 如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.
如图,在多面体ABCDEF中,底面ABCD是边长为2的菱形,∠BAD=60°,四边形BDEF是矩形,平面BDEF⊥平面ABCD,BF=3,H是CF的中点.(I)求证:BH∥平面AEF;
(Ⅱ)求EH与平面AFE所成角的正弦值.
分析 (I)建立如图所示的坐标系,求出平面AEF的法向量,利用$\overrightarrow{BH}$•$\overrightarrow{n}$=0,证明:BH∥平面AEF;
(Ⅱ)利用向量的夹角公式,求EH与平面AFE所成角的正弦值.
解答  (I)证明:建立如图所示的坐标系,则B(0,-1,0),C($\sqrt{3}$,0,0),F(0,-1,3),A(-$\sqrt{3}$,0,0),E(0,1,3),
(I)证明:建立如图所示的坐标系,则B(0,-1,0),C($\sqrt{3}$,0,0),F(0,-1,3),A(-$\sqrt{3}$,0,0),E(0,1,3),
∴H($\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$,$\frac{3}{2}$),
∴$\overrightarrow{BH}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,$\frac{3}{2}$),
设平面AEF的法向量为$\overrightarrow{n}$=(x,y,z),则
∵$\overrightarrow{AE}$=($\sqrt{3}$,1,3),$\overrightarrow{EF}$=(0,-2,0),
∴$\left\{\begin{array}{l}{\sqrt{3}x+y+3z=0}\\{-2y=0}\end{array}\right.$,
∴取$\overrightarrow{n}$=($\sqrt{3}$,0,-1),
∵$\overrightarrow{BH}$•$\overrightarrow{n}$=0
∴BH∥平面AEF;
(Ⅱ)解:$\overrightarrow{EH}$=($\frac{\sqrt{3}}{2}$,-$\frac{3}{2}$,-$\frac{3}{2}$),
∴EH与平面AFE所成角的正弦值=|$\frac{\frac{3}{2}+\frac{3}{2}}{\sqrt{3+1}•\sqrt{\frac{3}{4}+\frac{9}{4}+\frac{9}{4}}}$|=$\frac{\sqrt{21}}{7}$.
点评 本题考查空间向量知识的运用,考查线面平行,线面角,考查学生分析解决问题的能力,属于中档题.

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案| A. | a≥2+$\sqrt{3}$ | B. | 0<a<2-$\sqrt{3}$ | C. | a≥2+$\sqrt{3}$或0<a<1 | D. | a≥2+$\sqrt{3}$或0<a<2-$\sqrt{3}$ |
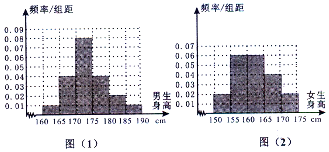 某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.(I)试问在抽取的学生中,男、女生各有多少人?
(II)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |