题目内容
14.数列{an}满足2an=an+1+an+1(n≥2),且a1+a3+a5=9,a2+a4+a6=12则a3+a4+a5=( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
分析 利用等差数列的通项公式及其性质即可得出.
解答 解:∵数列{an}满足2an=an+1+an+1(n≥2),∴数列{an}是等差数列,设公差为d.
∵a1+a3+a5=9,a2+a4+a6=12,
∴3d=3,解得d=1.
∴3a1+6d=9,解得a1=1.
∴an=1+(n-1)=n.
则a3+a4+a5=3+4+5=12.
故选:D.
点评 本题考查了等差数列的通项公式与性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.以椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的顶点为顶点,离心率为2的双曲线方程( )
| A. | $\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{27}$=1 | B. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{48}$=1或$\frac{{y}^{2}}{9}$-$\frac{{x}^{2}}{27}$=1 | ||
| C. | $\frac{{x}^{2}}{16}$-$\frac{{y}^{2}}{48}$=1 | D. | 以上都不对 |
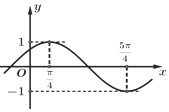 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.