题目内容
15.设命题p:f(x)=$\frac{1}{{\sqrt{a{x^2}-ax+1}}}$的定义域为R;命题q:不等式3x-9x<a-1对一切正实数x均成立.(1)如果命题p是真命题,求实数a的取值范围;
(2)如果命题p且q为真命题,求实数a的取值范围.
分析 (1)如果命题p是真命题,则a=0,或$\left\{\begin{array}{l}a>0\\{a}^{2}-4a<0\end{array}\right.$,解得实数a的取值范围;
(2)如果命题p且q为真命题,则命题p,q均为真命题,进而可得实数a的取值范围.
解答 解:(1)∵命题p是真命题,
∴a=0,或$\left\{\begin{array}{l}a>0\\{a}^{2}-4a<0\end{array}\right.$,
解得:a∈[0,4),
(2)若命题q:不等式3x-9x<a-1对一切正实数x均成立为真命题,
则a>3x-9x+1,令t=3x,y=-t2+t+1,
则当t=$\frac{1}{2}$时,函数取最大值$\frac{5}{4}$,
故a>$\frac{5}{4}$,
如果命题p且q为真命题,则命题p,q均为真命题,
∴a∈($\frac{5}{4}$,4).
点评 本题以命题的真假判断与应用为载体,考查了复合命题,函数的定义域,函数恒成立等知识点,难度中档.

练习册系列答案
相关题目
6.已知向量$\overrightarrow{a}$=(1,$\sqrt{3}$),$\overrightarrow{b}$=($\sqrt{3}$,1),则$\overrightarrow{a}$与$\overrightarrow{b}$夹角的大小为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
20.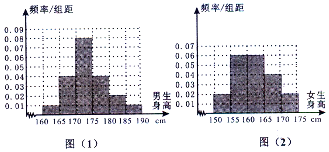 某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
(I)试问在抽取的学生中,男、女生各有多少人?
(II)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大的把握认为“身高与性别有关”?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
 某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.
某学校为调查高三年学生的身高情况,按随机抽样的方法抽取80名学生,得到男生身高情况的频率分布直方图(图(1)和女生身高情况的频率分布直方图(图(2)).已知图(1)中身高在170~175cm的男生人数有16人.(I)试问在抽取的学生中,男、女生各有多少人?
(II)根据频率分布直方图,完成下列的2×2列联表,并判断能有多大的把握认为“身高与性别有关”?
| ≥170cm | <170cm | 总计 | |
| 男生身高 | 30 | 10 | 40 |
| 女生身高 | 4 | 36 | 40 |
| 总计 | 34 | 46 | 80 |
| p(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.445 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.83 |
7.已知a>0,b>0,若不等式$\frac{mab}{3a+b}≤a+3b$恒成立,则m的最大值为( )
| A. | 4 | B. | 4 | C. | 12 | D. | 16 |