题目内容
13.已知函数f(x)=e2-x+x,x∈[1,3],则下列说法正确的是( )| A. | 函数f(x)的最大值为$3+\frac{1}{e}$ | B. | 函数f(x)的最小值为$3+\frac{1}{e}$ | ||
| C. | 函数f(x)的最大值为3 | D. | 函数f(x)的最小值为3 |
分析 求出函数f(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数f(x)的最小值即可.
解答 解:f(x)=e2-x+x,
f′(x)=-e2-x+1,
令f′(x)>0,解得:x>2,
令f′(x)<0,解得:x<2,
故f(x)在[1,2)递减,在(2,3]递增,
故f(x)的最小值是f(2)=3,
故选:D.
点评 本题考查了函数的单调性、最值问题,考查导数的应用,是一道基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.在正方体ABCD-A1B1C1D1中,M和N分别为A1B1和B1C1的中点,那么直线AM与CN所成角的余弦值是 ( )
| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{10}}}{10}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
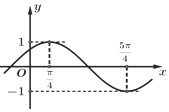 已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.
已知函数$f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<\frac{π}{2})$的部分图象如图所示.