题目内容
如图，平行四边形ABCD中，AE：EB=1：2，△AEF的面积为1cm2，则平行四边形ABCD的面积为考点：平行线分线段成比例定理
专题：演绎法
分析：由四边形ABCD为平行四边形，易判断出△AEF与△CDF相似，进而可得△AEF与△ABC的面积的比，结合△AEF的面积等于1cm2，即可求出平行四边形ABCD的面积．
解答：
解：∵AE∥CD，∴△AEF∽△CDF，
∴AE：CD=AF：CF，
∵AE：EB=1：2，
∴AE：AB=AE：CD=1：3，
∴AF：CF=1：3，
∴AF：AC=1：4，
∴△AEF与△ABC的高的比为1：4，
∴△AEF与△ABC的面积的比为1：12，
∴△AEF与平行四边形ABCD的面积的比为1：24，
∵△AEF的面积等于1cm2，
∴平行四边形ABCD的面积等于24cm2．
故答案为：24．
∴AE：CD=AF：CF，
∵AE：EB=1：2，
∴AE：AB=AE：CD=1：3，
∴AF：CF=1：3，
∴AF：AC=1：4，
∴△AEF与△ABC的高的比为1：4，
∴△AEF与△ABC的面积的比为1：12，
∴△AEF与平行四边形ABCD的面积的比为1：24，
∵△AEF的面积等于1cm2，
∴平行四边形ABCD的面积等于24cm2．
故答案为：24．
点评：本题考查相似三角形的判定，考查平行四边形面积的计算，判断出△AEF与△CDF相似，确定△AEF与△ABC的面积的比是关键．
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
已知f（x）是R上的奇函数，对x∈R都有f（x+4）=f（x）+f（2）成立，若f（1）=2，则f（2014）等于（ ）
| A、2014 | B、2 | C、0 | D、-2 |
函数f（x）=
x5-x4-4x3+7的极值点的个数是（ ）
| 1 |
| 5 |
| A、1个 | B、2个 | C、3个 | D、4个 |
在R上定义运算：对x、y∈R，有x⊕y=2x+y，如果a⊕（3b）=1，（ab＞0），则
⊕(
)的最小值是（ ）
| 1 |
| a |
| 1 |
| 3b |
| A、4 | ||
B、
| ||
| C、9 | ||
D、
|
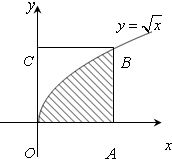在边长为1的正方形OABC中任取一点P，则点P恰好落在正方形与曲线y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|