题目内容
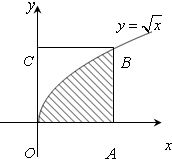 在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=
在边长为1的正方形OABC中任取一点P,则点P恰好落在正方形与曲线y=| x |
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型
专题:概率与统计
分析:欲求所投的点落在阴影部分内部的概率,须结合定积分计算阴影部分平面区域的面积,再根据几何概型概率计算公式易求解.
解答:
解:根据题意,正方形OABC的面积为1×1=1,而阴影部分的面积为
dx=
x
=
,
∴正方形OABC中任取一点P,点P取自阴影部分的概率为
=
,
故选B.
| ∫ | 1 0 |
| x |
| 2 |
| 3 |
| 2 |
| 3 |
| | | 1 0 |
| 2 |
| 3 |
∴正方形OABC中任取一点P,点P取自阴影部分的概率为
| ||
| 1 |
| 2 |
| 3 |
故选B.
点评:本题考查几何概型的计算,涉及定积分在求面积中的应用,关键是正确计算出阴影部分的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列函数中,在(0,+∞)上为增函数的是( )
| A、y=(x-1)2 | ||
| B、y=x2 | ||
C、y=(
| ||
D、y=
|
过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤9}分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
| A、x+y-2=0 |
| B、y-1=0 |
| C、x-y=0 |
| D、x+3y-4=0 |
若存在 x∈(-∞,0)使得方程2x-
-a=0成立,则实数a的取值范围是( )
| 1 |
| x-1 |
| A、(2,+∞) |
| B、(0,+∞) |
| C、(0,2) |
| D、(0,1) |
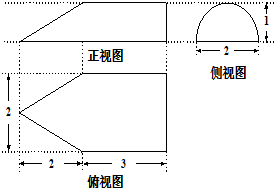
某几何体的三视图(如图),则该几何体的体积是( )

A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为
如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为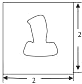 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为