题目内容
在[-6,9]内任取一个实数m,设f(x)=-x2+mx+m,则函数f(x)的图象与x轴有公共点的概率等于 .
考点:几何概型
专题:计算题,概率与统计
分析:利用f(x)=-x2+mx+m的图象与x轴有公共点,可得m<-4或m>0,根据在[-6,9]内任取一个实数m,以长度为测度,可求概率.
解答:
解:∵f(x)=-x2+mx+m的图象与x轴有公共点,
∴△=m2+4m>0,
∴m<-4或m>0,
∴在[-6,9]内任取一个实数m,函数f(x)的图象与x轴有公共点的概率等于
=
.
故答案为:
.
∴△=m2+4m>0,
∴m<-4或m>0,
∴在[-6,9]内任取一个实数m,函数f(x)的图象与x轴有公共点的概率等于
| |-4+6+9-0| |
| 9+6 |
| 11 |
| 15 |
故答案为:
| 11 |
| 15 |
点评:本题考查概率的计算,确定以长度为测度是关键.

练习册系列答案
相关题目
若圆(x-1)2+(y-2)2=5的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||
B、
| ||
| C、2或0 | ||
| D、-2或0 |
过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤9}分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
| A、x+y-2=0 |
| B、y-1=0 |
| C、x-y=0 |
| D、x+3y-4=0 |
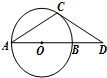 (几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若
(几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若 如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为
如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为 已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.