题目内容
在R上定义运算:对x、y∈R,有x⊕y=2x+y,如果a⊕(3b)=1,(ab>0),则
⊕(
)的最小值是( )
| 1 |
| a |
| 1 |
| 3b |
| A、4 | ||
B、
| ||
| C、9 | ||
D、
|
考点:基本不等式
专题:新定义
分析:由新定义结合已知得到2a+3b=1,再由新定义得到
⊕(
)的代数表达式,把1替换为2a+3b后利用基本不等式求最值.
| 1 |
| a |
| 1 |
| 3b |
解答:
解:由新定义运算对x、y∈R,有x⊕y=2x+y,结合a⊕(3b)=1,得2a+3b=1 (ab>0),
则
⊕(
)=
+
=
+
=4+
+
+1=5+
+
.
∵ab>0,
∴
>0,
>0,
则5+
+
≥5+2
=9(当且仅当
=
,即a=3b时取等号).
故选:C.
则
| 1 |
| a |
| 1 |
| 3b |
| 2 |
| a |
| 1 |
| 3b |
| 4a+6b |
| a |
| 2a+3b |
| 3b |
| 6b |
| a |
| 2a |
| 3b |
| 6b |
| a |
| 2a |
| 3b |
∵ab>0,
∴
| b |
| a |
| a |
| b |
则5+
| 6b |
| a |
| 2a |
| 3b |
|
| 6b |
| a |
| 2a |
| 3b |
故选:C.
点评:本题考查了基本不等式,训练了利用基本不等式求最值,利用基本不等式求最值时注意“一正、二定、三相等”,是中低档题.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
若圆(x-1)2+(y-2)2=5的圆心到直线x-y+a=0的距离为
,则a的值为( )
| ||
| 2 |
| A、-2或2 | ||
B、
| ||
| C、2或0 | ||
| D、-2或0 |
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
下列函数中,在(0,+∞)上为增函数的是( )
| A、y=(x-1)2 | ||
| B、y=x2 | ||
C、y=(
| ||
D、y=
|
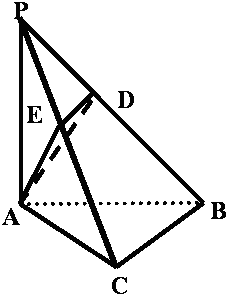 如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC
如图,在三梭锥P-ABC中,PA⊥底面ABC,PA=AB=2,∠ABC=60°,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC 如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为
如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为 已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.