题目内容
已知f（x）是R上的奇函数，对x∈R都有f（x+4）=f（x）+f（2）成立，若f（1）=2，则f（2014）等于（ ）
| A、2014 | B、2 | C、0 | D、-2 |
考点：函数的周期性
专题：函数的性质及应用
分析：利用函数奇偶性的性质求出函数是周期函数即可得到结论．
解答：
解：∵f（x）是R上的奇函数，对x∈R都有f（x+4）=f（x）+f（2）成立，
∴可令x=-2，则f（-2+4）=f（-2）+f（2），
解得f（-2）=0，而f（-2）=-f（2），
∴f（2）=0．
∴f（x+4）=f（x）．
∴f（2014）=f（503×4+2）=f（2）=0．
故选：C．
∴可令x=-2，则f（-2+4）=f（-2）+f（2），
解得f（-2）=0，而f（-2）=-f（2），
∴f（2）=0．
∴f（x+4）=f（x）．
∴f（2014）=f（503×4+2）=f（2）=0．
故选：C．
点评：本题考查了函数的奇偶性、周期性，属于基础题．
练习册系列答案
相关题目
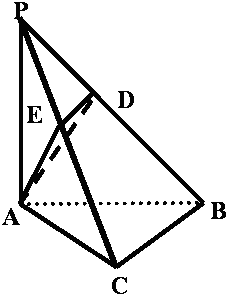如图，在三梭锥P-ABC中，PA⊥底面ABC，PA=AB=2，∠ABC=60°，∠BCA=90°，点D、E分别在棱PB、PC上，且DE∥BC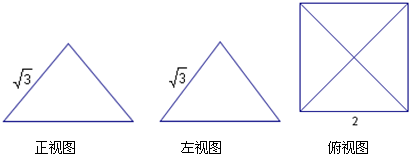
某单位拟建一个扇环面形状的花坛（如图所示），该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成．按设计要求扇环面的周长为30米，其中大圆弧所在圆的半径为10米．设小圆弧所在圆的半径为x米，圆心角为θ（弧度）．
如图，平行四边形ABCD中，AE：EB=1：2，△AEF的面积为1cm2，则平行四边形ABCD的面积为下列函数中，在（0，+∞）上为增函数的是（ ）
| A、y=（x-1）2 | ||
| B、y=x2 | ||
C、y=（
| ||
D、y=
|