题目内容
偶函数f(x)满足f(x-1)=f(x+1),且在x∈[0,1]时,f(x)=1-x,则关于x的方程f(x)=log9(x+1)解的个数是 个.
考点:对数函数图象与性质的综合应用
专题:函数的性质及应用
分析:根据函数的奇偶性、单调性和周期性画出函数f(x)和y=log9(x+1)的图象,观察图象交点个数,进而即可得到答案.
解答:
解:①设x∈[-1,0],则(-x)∈[0,1],
又∵函数f(x)是偶函数,
∴f(x)=f(-x)=-(x+1).
由函数f(x)满足f(x-1)=f(x+1),
∴f(x)=f(x+2),
∴函数f(x)是周期为2的函数.
因此可以先画出y=f(x)在区间[-1,1]上的图象,根据周期性即可画出整个定义域内的图象.
②画出g(x)=log9(x+1)的图象,

由图象和上面的分析可知:函数y=f(x) 与y=g(x)有且仅有8个交点,即关于x的方程f(x)=log9(x+1)解的个数是8.
故答案为:8

又∵函数f(x)是偶函数,
∴f(x)=f(-x)=-(x+1).
由函数f(x)满足f(x-1)=f(x+1),
∴f(x)=f(x+2),
∴函数f(x)是周期为2的函数.
因此可以先画出y=f(x)在区间[-1,1]上的图象,根据周期性即可画出整个定义域内的图象.
②画出g(x)=log9(x+1)的图象,

由图象和上面的分析可知:函数y=f(x) 与y=g(x)有且仅有8个交点,即关于x的方程f(x)=log9(x+1)解的个数是8.
故答案为:8
点评:本题考查的知识点是对数函数的图象和性质,函数的奇偶性,函数的周期性,熟练掌握函数的奇偶性、单调性和周期性及画出图象是解题的关键.

练习册系列答案
相关题目
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
 某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度).
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点O为圆心的两个同心圆弧和延长后通过点O的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为x米,圆心角为θ(弧度). 如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为
如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为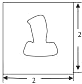 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为