题目内容
已知f(x)在(-1,1)上有定义,f(
)=1,且满足x,y∈(-1,1)时有f(x)-f(y)=f(
),数列{xn}满足x1=
,xn+1=
.
(1)求f(0)的值,并证明f(x)在(-1,1)上为奇函数;
(2)探索f(xn+1)与f(xn)的关系式,并求f(xn)的表达式;
(3)是否存在自然数m,使得对于任意的n∈N*,
+
+…+
>
恒成立?若存在,求出m的最大值.
| 1 |
| 2 |
| x-y |
| 1-xy |
| 1 |
| 2 |
| 2xn |
| 1+xn2 |
(1)求f(0)的值,并证明f(x)在(-1,1)上为奇函数;
(2)探索f(xn+1)与f(xn)的关系式,并求f(xn)的表达式;
(3)是否存在自然数m,使得对于任意的n∈N*,
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| m-8 |
| 4 |
考点:抽象函数及其应用
专题:综合题,函数的性质及应用
分析:(1)令x=y⇒f(0)=0,再令x=0⇒f(-y)=-f(y),从而可证f(x)在(-1,1)上为奇函数;
(2)依题意,可求得f(xn+1)=2f(xn),f(x1)=f(
)=1,q=2,于是可求得f(xn)的表达式;
(3)由f(xn)=2n-1⇒
=(
)n-1,利用等比数列的求和公式可求得
+
+…+
=2-(
)n-1,再解不等式2-(
)n-1>
,即可求得m的最大值.
(2)依题意,可求得f(xn+1)=2f(xn),f(x1)=f(
| 1 |
| 2 |
(3)由f(xn)=2n-1⇒
| 1 |
| f(xn) |
| 1 |
| 2 |
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
| 1 |
| 2 |
| 1 |
| 2 |
| m-8 |
| 4 |
解答:
解:(1)令x=y⇒f(0)=0,
令x=0⇒f(0)-f(y)=f(
)=f(-y),
∴f(-y)=-f(y).
∴f(x)在(-1,1)上为奇函数.
(2)∵f(xn+1)=f(
)=f(
)=f(xn)-f(-xn)=2f(xn),
∴
=2(常数),
∴{f(xn)}为等比数列.
又f(x1)=f(
)=1,q=2,
∴f(xn)=2n-1.
(3)假设存在自然数m满足题设条件,
则
+
+…+
=1+
+(
)2+…+(
)n-1
=
=2-(
)n-1>
对于任意的n∈N*成立,
∴m<16-
对于任意的n∈N*成立,
当n=1时,16-
的最小值为12,
∴m<12,即m的最大值为11.
令x=0⇒f(0)-f(y)=f(
| 0-y |
| 1-0×y |
∴f(-y)=-f(y).
∴f(x)在(-1,1)上为奇函数.
(2)∵f(xn+1)=f(
| 2xn |
| 1+xn2 |
| xn-(-xn) |
| 1-xn(-xn) |
∴
| f(xn+1) |
| f(xn) |
∴{f(xn)}为等比数列.
又f(x1)=f(
| 1 |
| 2 |
∴f(xn)=2n-1.
(3)假设存在自然数m满足题设条件,
则
| 1 |
| f(x1) |
| 1 |
| f(x2) |
| 1 |
| f(xn) |
=1+
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=
1-(
| ||
1-
|
=2-(
| 1 |
| 2 |
| m-8 |
| 4 |
∴m<16-
| 8 |
| 2n |
当n=1时,16-
| 8 |
| 2n |
∴m<12,即m的最大值为11.
点评:本题考查抽象函数及其应用,着重考查赋值法与等比关系的确定,突出考查等比数列的求和与函数性质的综合应用,属于难题.

练习册系列答案
相关题目
在棱长为2的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去8个三棱锥后,剩下的几何体的体积是( )
A、
| ||
| B、8 | ||
C、
| ||
D、
|
下列函数中,在(0,+∞)上为增函数的是( )
| A、y=(x-1)2 | ||
| B、y=x2 | ||
C、y=(
| ||
D、y=
|
某几何体的三视图(如图),则该几何体的体积是( )
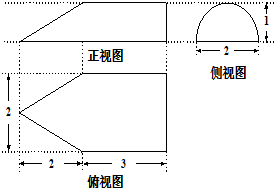

A、
| ||
B、
| ||
C、
| ||
D、
|
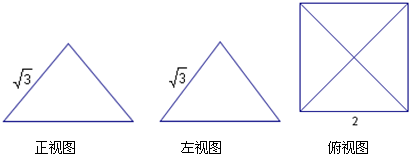
 如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为
如图,平行四边形ABCD中,AE:EB=1:2,△AEF的面积为1cm2,则平行四边形ABCD的面积为 已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.
已知直角三角形ABC,其中∠ABC=60°,∠C=90°,AB=2,求△ABC绕斜边AB旋转一周所形成的几何体的表面积和体积.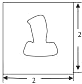 某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为
某人为估算图中图中不规则图形的面积,将其放置在边长为2的正方形内,然后借助计算机随机向正方形内抛掷1000个点,得知落在不规则图形内的点共有250个,则图中不规则图形的面积约为