题目内容

（1）画出不等式组
x-4y≤-4  
3x+5y≤15  
x≥1  
表示的平面区域．
（2）A={x|x2-x-6＜0}，B={x|x2+2x-8＞0}，求A∩B．
考点：简单线性规划,交集及其运算
专题：不等式的解法及应用
分析：（1）利用直线定边界，特殊点定区域，画出不等式组
x-4y≤-4  
3x+5y≤15  
x≥1  
表示的平面区域．
（2）求出集合A={x|x2-x-6＜0}，与集合B={x|x2+2x-8＞0}，即可求A∩B．
解答： 解：（1）不等式组
x-4y≤-4  
3x+5y≤15  
x≥1  
表示的平面区域如图：阴影部分．
（2）A={x|x2-x-6＜0}={x|-2＜x＜3}，
B={x|x2+2x-8＞0}={x|x＜-4或x＞2}，
则A∩B={x|2＜x＜3}．
点评：本题考查简单的线性规划，二次不等式的解法，交集的运算．
练习册系列答案
相关题目
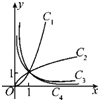图中的曲线是幂函数y=xn在第一象限的图象，已知n可取±2，±
1
2
四个值，则对应于曲线C1、C2、C3、C4的n依次为（　　）
A、-2，-
1
2
，
1
2
，2
B、2，
1
2
，-
1
2
，-2
C、-
1
2
，-2，2，
1
2
D、2，
1
2
，-2，-
1
2
已知x，y＞0，x+2y=10，求ω=x2+y2的最小值．
已知
a
=（4，3），
b
=（-1，2），
m
=
a
-λ
b
，
n
=2
a
+
b
，按下列条件求λ值．
（1）
m
⊥
n
；　　　　
（2）
m
∥
n
．
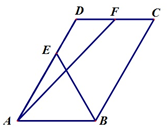已知平行四边形ABCD中，|
AB
|=4，|
AD
|=6，∠DAB=
π
3
，
AE
=
2
3
AD
，
DF
=
FC
．
（1）求
AF
•
BE
的值．
（2）求向量
AF
与向量
BE
的夹角θ的余弦值．
已知椭圆C：
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率为
5
3
，连接椭圆的四个顶点得到的菱形的面积为12．
（1）求椭圆的面积；
（2）若点M、N在椭圆上，点E（1，1）为MN的中点，求出直线MN所在的方程．
已知函数g（x）=
1
4x+2
（x∈R）．
（1）求：g（x）+g（1-x）的值；
（2）求：g（
1
m
）+g（
2
m
）+g（
3
m
）+…+g（
m-1
m
）+g（
m
m
）的值．
（3）设函数f（x）=-g（-log16x），a，b为常数且0＜a＜b，在下列四个不等关系中选出一个你认为正确的关系式，并加以说明．
①f（a）＜f（
a+b
2
）＜f（ab）        
②f（a）＜f（b）＜f（
ab
）
③f（
ab
）＜f（
a+b
2
）＜f（a）      
④f（b）＜f（
a+b
2
）＜f（
ab
）．
已知数列{an}的前n项和是Sn 且Sn=2n2，数列{bn}的前n项和是Tn且Tn+
1
2
bn=1．n∈N*
（1）求数列{an}的通项公式；
（2）求证：数列{bn}是等比数列；
（3）记cn=
1
4
an•bn，求数列{cn}的前n项和Mn．
已知函数f（x）=sin2x+2cos2x．
（Ⅰ）求函数的周期；
（Ⅱ）求f（x）的最大值及对应的x值的集合．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网