题目内容

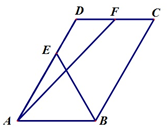已知平行四边形ABCD中，|
AB
|=4，|
AD
|=6，∠DAB=
π
3
，
AE
=
2
3
AD
，
DF
=
FC
．
（1）求
AF
•
BE
的值．
（2）求向量
AF
与向量
BE
的夹角θ的余弦值．
考点：数量积表示两个向量的夹角
专题：平面向量及应用
分析：（1）由条件求得
AB
•
AD
 的值，可得
AF
•
BE
=（
AD
+
1
2
AB
）•（
2
3
AD
-
AB
） 的值．
（2）先求得|
AF
|=
(
AD
+
1
2
AB
)2
和|
BE
|=
(
2
3
AD
-
AB
)2
的值，可得cosθ=
AF
•
BE
|
AF
|•|
BE
|
 的值．
解答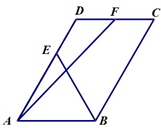： 解：（1）由题意可得，
AB
•
AD
=4×6×cos
π
3
=12，
AF
•
BE
=（
AD
+
DF
）•（
AE
-
AB
）=（
AD
+
1
2
AB
）•（
2
3
AD
-
AB
）
=
2
3
AD
2-
1
2
AB
2-
2
3
AB
•
AD
=24-8-8=8．
（2）由于|
AF
|=
(
AD
+
1
2
AB
)2
=
AD
2+
AB
2
4
+
AB
•
AD
=2
13
，
|
BE
|=|
2
3
AD
-
AB
|=
(
2
3
AD
-
AB
)2
=4，
故向量
AF
与向量
BE
的夹角θ的余弦值cosθ=
AF
•
BE
|
AF
|•|
BE
|
=
8
2
13
×4
=
13
13
．
点评：本题主要考查两个向量的加减法的法则，以及其几何意义，用数量积表示两个两个向量的夹角，属于较基础题．
练习册系列答案
相关题目
过已知点A（2，3），B（1，5）的直线AB的斜率是（　　）
A、2
B、-2
C、
1
2
D、-
1
2
已知数列{an}的前n项和为Sn，且满足Sn=2an-n，（n∈N*）
（1）求数列{an}的通项公式；
（2）若bn=（2n+1）an+2n+1，数列{bn}的前n项和为Tn，求满足不等式
Tn-2
2n-1
≥128的最小n值．
已知函数f（x）=-
1
3
x3+4x-4．
（Ⅰ）求函数f（x）的极值；
（Ⅱ）求函数f（x）在区间[-1，3]上的最值．
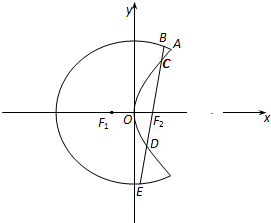如图，曲线C1是以原点O为中心、F1，F2为焦点的椭圆的一部分，曲线C2是以O为顶点、F2为焦点的抛物线的一部分，A是曲线C1和C2的交点且∠AF2F1为钝角，我们把由曲线C1和曲线C2合成的曲线C称为“月蚀圆”．若|AF1|=7，|AF2|=5．
（Ⅰ）求曲线C1和C2所在的椭圆和抛物线方程；
（Ⅱ）过F2作一条与x轴相交的直线l，分别与“月蚀圆”依次交于B、C、D、E四点，
（1）当直线l⊥x轴时，求
|CD|
|BE|
的值；
（2）当直线l不垂直x轴时，若G为CD中点、H为BE中点，问
|CD|•|HF2|
|BE|•|GF2|
是否为定值？若是，求出此定值；若不是，请说明理由．
（1）画出不等式组
x-4y≤-4  
3x+5y≤15  
x≥1  
表示的平面区域．
（2）A={x|x2-x-6＜0}，B={x|x2+2x-8＞0}，求A∩B．
求函数f（x）=x3-3x2在区间[-1，5]上的最值．
已知椭圆方程为
x2
a2
+
y2
b2
=1（a＞b＞0），它的一个顶点为M（0，1），离心率e=
6
3
．
（Ⅰ）求椭圆方程；
（Ⅱ）过点M分别作直线MA，MB交椭圆于A，B两点，设两直线的斜率分别为k1，k2，且k1+k2=3．求证：直线AB过定点，并求出直线AB的斜率k的取值范围．
双曲线E与椭圆
x2
25
+
y2
16
=1有公共焦点，且离心率为
3
2
．
（1）求双曲线E的方程；
（2）若斜率为1的直线l交双曲线E于A、B两点，且|AB|=4
30
，求l方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网