题目内容
17．若关于x的不等式|x-m|+|x+2|＞4的解集为R，则实数m的取值范围是（ ）| A． | （-2，6） | B． | （-∞，-6）∪（2，+∞） | C． | （-∞，-2）∪（6，+∞） | D． | （-6，2） |
分析 由绝对值的意义可得|x-m|+|x+2|的最小值等于|2+m|，由题意可得|2+m|＞4，由此解得实数m的取值范围．
解答 解：由|x-m|+|x+2|≥|x-m-x-2|=|m+2|，它的最小值等于|2+m|，
由题意可得|2+m|＞4，解得m＞2，或 m＜-6，
故选：B．
点评 本题主要考查绝对值的意义，绝对值不等式的解法，得到|2+m|＞4是解题的关键，属于中档题．
练习册系列答案
口算能手系列答案
相关题目
12．
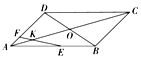如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）
如图，平行四边形ABCD的两条对角线相交于点O，点E、F分别在边AB、AD上，$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$，$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$，直线EF交于AC于点K，$\overrightarrow{AK}$=λ$\overrightarrow{AO}$，则λ等于（ ）| A． | $\frac{8}{27}$ | B． | $\frac{1}{3}$ | C． | $\frac{10}{27}$ | D． | $\frac{11}{27}$ |
2．禽流感是家禽养殖业的最大威胁．为检验某新药物预防禽流感的效果，取80只家禽进行试验，得到如下丢失数据的列联表：（c，d，M，N表示丢失的数据）
（1）求出a，b，d，M，N的值，并判断：能否有99.5%的把握认为药物有效；
（2）若表中服用药后患病的5只家禽分别为3只鸡和2只鸭，现从这5只家禽中随机选取2只，求这2只家禽是同一类的概率．
下面的临界值表供参考：
（参考公式：K2=$\frac{{n（ad-bc）}^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
| 患病 | 未患病 | 总计 | |
| 未服用药 | a | b | 40 |
| 服用药 | 5 | d | M |
| 总计 | 25 | N | 80 |
（2）若表中服用药后患病的5只家禽分别为3只鸡和2只鸭，现从这5只家禽中随机选取2只，求这2只家禽是同一类的概率．
下面的临界值表供参考：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |