题目内容
12.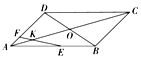 如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{10}{27}$ | D. | $\frac{11}{27}$ |
分析 根据向量的加减的几何意义和三点共线即可求出答案.
解答 解:∵$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,
∴$\overrightarrow{AK}$=λ$\overrightarrow{AO}$=$\frac{1}{2}$λ($\overrightarrow{AB}$+$\overrightarrow{AD}$)=$\frac{1}{2}λ$($\frac{7}{5}$$\overrightarrow{AE}$+4$\overrightarrow{AF}$)=$\frac{7λ}{10}$$\overrightarrow{AE}$+2λ$\overrightarrow{AF}$,
∵三点E,F,K共线,
∴$\frac{7λ}{10}$+2λ=1,
∴λ=$\frac{10}{27}$,
故选:C
点评 本题考查了平面向量的线性运算,及三点共线的充要条件,属于中档题.

练习册系列答案
相关题目
2. 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
( )
 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{2}$ |
3. 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
| A. | 100$\sqrt{2}$米 | B. | 50($\sqrt{3}$+1)米 | C. | $100({\sqrt{3}+1})$米 | D. | 200米 |
17.若关于x的不等式|x-m|+|x+2|>4的解集为R,则实数m的取值范围是( )
| A. | (-2,6) | B. | (-∞,-6)∪(2,+∞) | C. | (-∞,-2)∪(6,+∞) | D. | (-6,2) |
4.己知数列{an}是等比数列,b1009是1和3的等差中项,则b1b2017=( )
| A. | 16 | B. | 8 | C. | 2 | D. | 4 |
2.某家庭连续五年收入x与支出y如表:
画散点图知:y与x线性相关,且求得的回归方程是y=bx+a,其中b=0.76,则据此预计该家庭2017年若收入15万元,支出为( )万元.
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 收入(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4 | B. | 11.8 | C. | 12.0 | D. | 12.2 |