��Ŀ����
6����ֱ������ϵxOy�У�����C1�IJ�������Ϊ$\left\{\begin{array}{l}x=1+acost\\ y=asint\end{array}$��tΪ������a��0������������ԭ��Ϊ���㣬x��������Ϊ����ļ�����ϵ�У�����C2����=2sin�ȣ���1��������C1����ͨ���̣�����C1�ķ��̻�Ϊ�����귽�̣�
��2��ֱ��C3�ļ����귽��Ϊ��=$\frac{��}{4}$��������C1��C2�Ĺ����㶼��C3�ϣ���a��ֵ��
���� ��1���������ַ��̵�ת������������C1����ͨ���̣�����C1�ķ��̻�Ϊ�����귽�̣�
��2������C1��C2�Ĺ�����ļ��������㷽����$\left\{\begin{array}{l}{��^2}-2��cos��+1-{a^2}=0\\ ��=2sin��\end{array}\right.$�����ѡ�0���ɷ������4sin2��-4sin��cos��+1-a2=0������֪$��=\frac{��}{4}$��������a��ֵ��
��� �⣺��1����ȥ����t�õ�C1����ͨ���̣�x-1��2+y2=a2����x=��cos�ȣ�y=sin�ȴ���C1����ͨ���̣��õ�C1�ļ����귽�̣���2-2��cos��+1-a2=0��
��2������C1��C2�Ĺ�����ļ��������㷽����$\left\{\begin{array}{l}{��^2}-2��cos��+1-{a^2}=0\\ ��=2sin��\end{array}\right.$�����ѡ�0��
�ɷ������4sin2��-4sin��cos��+1-a2=0������֪$��=\frac{��}{4}$���ɽ��1-a2=0��
����a��0���õ�a=1����a=1ʱ������ҲΪC1��C2�Ĺ����㶼��C3�ϣ�����a=1��
���� ���⿼�˲������̺ͼ����귽�̵�Ӧ�ã������˼�������ֱ������Ļ������ǻ����⣮

��ϰ��ϵ�д�
 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
�����Ŀ
16������A��4��3����B��2��-1����ֱ��x+2y-a=0�����࣬��a��ȡֵ��Χ�ǣ�������
| A�� | ��0��10�� | B�� | ��-1��2�� | C�� | ��0��1�� | D�� | ��1��10�� |
17��������x�IJ���ʽ|x-m|+|x+2|��4�Ľ⼯ΪR����ʵ��m��ȡֵ��Χ�ǣ�������
| A�� | ��-2��6�� | B�� | ��-�ޣ�-6���ȣ�2��+�ޣ� | C�� | ��-�ޣ�-2���ȣ�6��+�ޣ� | D�� | ��-6��2�� |
15����֪ʵ��x��y���㲻��ʽ��$\left\{\begin{array}{l}x+y-5��0\\ x-2y+1��0\\ x��1\end{array}\right.$��������ʽy2-2xy��ax2���������ʵ��a����СֵΪ��������
| A�� | 8 | B�� | 3 | C�� | -1 | D�� | -6 |
6����֪����p��log2��x-1����1�Ľ⣬q��x2-2x-3��0�Ľ⣬��p��q�ģ�������������
| A�� | ��ַDZ�Ҫ | B�� | ��Ҫ�dz�� | ||
| C�� | ��ֱ�Ҫ | D�� | �ȷdz���ַDZ�Ҫ |


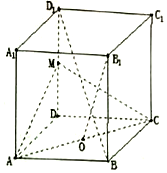 ��������ABCD-A1B1C1D1�У�MΪDD1���е㣬OΪAC���е㣬AB=1��
��������ABCD-A1B1C1D1�У�MΪDD1���е㣬OΪAC���е㣬AB=1��