题目内容
7.设复数z=a+bi(a,b∈R,a>0,i是虚数单位),且复数z满足|z|=$\sqrt{10}$,复数(1+2i)z在复平面上对应的点在第一、三象限的角平分线上.(1)求复数z;
(2)若$\overline{z}$+$\frac{m-i}{1+i}$为纯虚数(其中m∈R),求实数m的值.
分析 (1)直接由题意列关于a,b的方程组,求解得答案;
(2)把z代入$\overline{z}$+$\frac{m-i}{1+i}$,利用复数代数形式的乘除运算化简,再由实部为0且虚部不为0求得m的值.
解答 解:(1)由(1+2i)z=(1+2i)(a+bi)=(a-2b)+(2a+b)i
在复平面上对应的点在第一、三象限的角平分线上,
得a-2b=2a+b,∴a=-3b,
又|z|=$\sqrt{10}$,得a2+b2=10.
联立解得:$\left\{\begin{array}{l}{a=3}\\{b=-1}\end{array}\right.$或$\left\{\begin{array}{l}{a=-3}\\{b=1}\end{array}\right.$.
∵a>0,∴z=3-i;
(2)∵$\overline{z}$+$\frac{m-i}{1+i}$=3+i+$\frac{m-i}{1+i}$=3+i+$\frac{(m-i)(1-i)}{(1+i)(1-i)}$=$3+i+\frac{m-1-(m+1)i}{2}$=$\frac{m+5}{2}-\frac{m-1}{2}i$为纯虚数,
∴m=-5.
点评 本题考查复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.函数f(x)=x2-2x+a在区间(1,3)内有一个零点,则实数a的取值范围是( )
| A. | (-3,0) | B. | (-3,1) | C. | (-1,3) | D. | (-1,1) |
2. 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
( )
 如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=
如图,已知△OAB,若点C满足$\overrightarrow{AC}=2\overrightarrow{CB},\overrightarrow{OC}=λ\overrightarrow{OA}+μ\overrightarrow{OB}(λ,μ∈R)$,则$\frac{1}{λ}+\frac{1}{μ}$=( )
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{2}{9}$ | D. | $\frac{9}{2}$ |
19.已知集合A={x|2x-5>0},B={x|x2-4x+3≤0},则A∩B=( )
| A. | (1,$\frac{5}{2}$) | B. | [1,$\frac{5}{2}$) | C. | ($\frac{5}{2}$,3) | D. | ($\frac{5}{2}$,3] |
16.若点A(4,3),B(2,-1)在直线x+2y-a=0的两侧,则a的取值范围是( )
| A. | (0,10) | B. | (-1,2) | C. | (0,1) | D. | (1,10) |
17.若关于x的不等式|x-m|+|x+2|>4的解集为R,则实数m的取值范围是( )
| A. | (-2,6) | B. | (-∞,-6)∪(2,+∞) | C. | (-∞,-2)∪(6,+∞) | D. | (-6,2) |
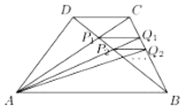 梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)
梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)