题目内容
8.(1)设α,β为锐角,且$sinα=\frac{{\sqrt{5}}}{5},cosβ=\frac{{3\sqrt{10}}}{10}$,求α+β的值;(2)化简求值:$sin50°(1+\sqrt{3}tan10°)$.
分析 (1)利用同角三角函数的基本关系、两角和差的余弦公式求得 cos(α+β)的值,结合α+β的范围,可得α+β的值.
(2)利用同角三角函数的基本关系、两角和差的三角公式、诱导公式,求得所给式子的值.
解答 解:(1)∵α为锐角,$sinα=\frac{{\sqrt{5}}}{5}$,∴$cosα=\frac{{2\sqrt{5}}}{5}$;∵β为锐角,$cosβ=\frac{{3\sqrt{10}}}{10}$,∴$sinβ=\frac{{\sqrt{10}}}{10}$,
∴cos(α+β)=cosαcosβ-sinαsinβ=$\frac{{2\sqrt{5}}}{5}×\frac{{3\sqrt{10}}}{10}-\frac{{\sqrt{5}}}{5}×\frac{{\sqrt{10}}}{10}=\frac{{\sqrt{2}}}{2}$,∵α+β∈(0,π),∴α+β=$\frac{π}{4}$.
(2)$sin50°(1+\sqrt{3}tan10°)$=$\frac{sin50°•(cos10°+\sqrt{3}sin10°)}{cos10°}$=sin50°•$\frac{2cos(60°-10°)}{cos10°}$=$\frac{sin100°}{cos10°}$=1.
点评 本题主要考查同角三角函数的基本关系、两角和差的余弦公式、诱导公式的应用,属于基础题.

练习册系列答案
相关题目
19.已知集合A={x|2x-5>0},B={x|x2-4x+3≤0},则A∩B=( )
| A. | (1,$\frac{5}{2}$) | B. | [1,$\frac{5}{2}$) | C. | ($\frac{5}{2}$,3) | D. | ($\frac{5}{2}$,3] |
16.若点A(4,3),B(2,-1)在直线x+2y-a=0的两侧,则a的取值范围是( )
| A. | (0,10) | B. | (-1,2) | C. | (0,1) | D. | (1,10) |
3. 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
 如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的
如图,D,C,B三点在地面同一直线上,从地面上C,D两点望山顶A,测得它们的仰角分别为45°和30°,已知CD=200米,点C位于BD上,则山高AB等于( )
| A. | 100$\sqrt{2}$米 | B. | 50($\sqrt{3}$+1)米 | C. | $100({\sqrt{3}+1})$米 | D. | 200米 |
17.若关于x的不等式|x-m|+|x+2|>4的解集为R,则实数m的取值范围是( )
| A. | (-2,6) | B. | (-∞,-6)∪(2,+∞) | C. | (-∞,-2)∪(6,+∞) | D. | (-6,2) |
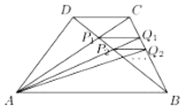 梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)
梯形ABCD中AB∥CD,对角线AC,BD交于P1,过P1作AB的平行线交BC于点Q1,AQ1交BD于P2,过P2作AB的平行线交BC于点Q2,….,若AB=a,CD=b,则PnQn=$\frac{ab}{a+nb},n∈N*$(用a,b,n表示)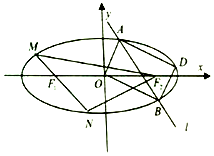 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),短轴长2,两焦点分别为F1,F2,过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0),短轴长2,两焦点分别为F1,F2,过F1的直线交椭圆C于M,N两点,且△F2MN的周长为8.