题目内容
已知函数f(x)=x2+2x+1,若存在实数t,使得不等式f(x+t)≤x对任意的x∈[1,m](m>1)恒成立,则实数m的最大值为 .
考点:函数恒成立问题
专题:函数的性质及应用,不等式的解法及应用
分析:由当x∈[1,m]时,f(x+t)≤x恒成立,即g(x)=f(x+t)-x≤0恒成立,则需满足g(1)≤0且g(m)≤0,解出t的范围,讨论m的取值即可得到m的最大值.
解答:
解:设g(x)=f(x+t)-x=x2+(2t+1)x+(1+t)2,
由题意f(x+t)-x≤0对任意的x∈[1,m](m>1)恒成立,
即g(1)≤0且g(m)≤0.
由g(1)≤0,得t∈[-3,-1],
由g(m)≤0,得m2+(2t+1)m+(t+1)2≤0,
则当t=-1时,得到m2-m≤0,解得0≤m≤1;
当t=-3时,得到m2-5m+4≤0,解得1≤m≤4.
综上得到:m∈[1,4],
∴m的最大值为4.
故答案为:4.
由题意f(x+t)-x≤0对任意的x∈[1,m](m>1)恒成立,
即g(1)≤0且g(m)≤0.
由g(1)≤0,得t∈[-3,-1],
由g(m)≤0,得m2+(2t+1)m+(t+1)2≤0,
则当t=-1时,得到m2-m≤0,解得0≤m≤1;
当t=-3时,得到m2-5m+4≤0,解得1≤m≤4.
综上得到:m∈[1,4],
∴m的最大值为4.
故答案为:4.
点评:本题考查学生理解函数恒成立时取条件的能力,体现了数学转化思想方法,训练了灵活运用二次函数求最值的方法的能力,是中档题.

练习册系列答案
相关题目
若0≤x≤3,则y=x2-4x+3( )
| A、有最小值0,最大值3 |
| B、有最小值-1,最大值0 |
| C、有最小值-1,最大值1 |
| D、有最小值-1,最大值3 |
下列说法一定正确的是( )
| A、若ab>ac,则b>c | ||||
| B、若a>b,c>d,则ac>bd | ||||
C、若a>b,则
| ||||
| D、若a>b,则a+c>b+c |
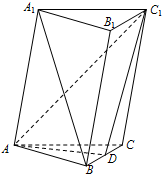 如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.
如图,已知斜三棱柱ABC-A1B1C1中,AB=AC,D为BC的中点.