题目内容
若0≤x≤3，则y=x2-4x+3（ ）
| A、有最小值0，最大值3 |
| B、有最小值-1，最大值0 |
| C、有最小值-1，最大值1 |
| D、有最小值-1，最大值3 |
考点：二次函数的性质
专题：函数的性质及应用
分析：先将解析式配方，再判断出函数在区间上的单调性，利用单调性求出函数的最大值、最小值．
解答：
解：由题意得，y=x2-4x+3=（x-2）2-1，
所以函数在x∈[0，2]单调递减，在x∈[2，3]单调递增，
所以fmin（x）=f（2）=-1，fmax（x）=f（0）=3．
故选：D．
所以函数在x∈[0，2]单调递减，在x∈[2，3]单调递增，
所以fmin（x）=f（2）=-1，fmax（x）=f（0）=3．
故选：D．
点评：本题考查二次函数的单调性、最值，一般利用配方法化简解析式，属于基础题．
练习册系列答案
相关题目
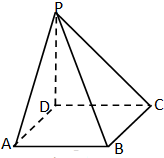四棱锥P-ABCD中，底面ABCD是边长为2的正方形，且PA⊥底面ABCD，PA=2AB，则四棱锥P-ABCD外接球的表面积为（ ）| A、24π | B、8π |
| C、6π | D、36π |