题目内容
在等差数列{an}中,若S4=1,S8=4,则a17+a18+a19+a20的值为( )
| A、9 | B、12 | C、16 | D、17 |
考点:等差数列的通项公式
专题:等差数列与等比数列
分析:设出等差数列的首项和公差,得到前n项和,由已知列式求得首项和公差,把a17+a18+a19+a20转化为含首项和公差的表达式得答案.
解答:
解:设首项为a1,公差为d.
由Sn=na1+
,得
S4=4a1+6d=1,
S8=8a1+28d=4,
解得:a1=
,d=
.
∴a17+a18+a19+a20=S20-S16=4a1+70d
=4×
+70×
=9.
故选A.
由Sn=na1+
| n(n-1)d |
| 2 |
S4=4a1+6d=1,
S8=8a1+28d=4,
解得:a1=
| 1 |
| 16 |
| 1 |
| 8 |
∴a17+a18+a19+a20=S20-S16=4a1+70d
=4×
| 1 |
| 16 |
| 1 |
| 8 |
故选A.
点评:本题考查了等差数列的通项公式,考查了等差数列的前n项和,是基础的计算题.

练习册系列答案
相关题目
直线y=3x+6与两坐标轴围成的三角形的面积是( )
| A、4 | B、5 | C、6 | D、7 |
已知A={x|x2-4x+3≥0},B={x|x≤0或x≥4},则( )
| A、A?B | B、B?A |
| C、A=B | D、A∩B=∅ |
 已知程序如图所示.
已知程序如图所示.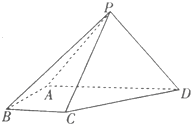 如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=