题目内容
已知A={x|x2-4x+3≥0}，B={x|x≤0或x≥4}，则（ ）
| A、A?B | B、B?A |
| C、A=B | D、A∩B=∅ |
考点：集合的包含关系判断及应用
专题：不等式的解法及应用,集合
分析：先求出x2-4x+3≥0的解集A，再由子集的定义判断出A、B的关系．
解答：
解：由x2-4x+3≥0得，x≤1或x≥3，则集合A={x|x≤1或x≥3}，
又B={x|x≤0或x≥4}，则B?A，
故选：B．
又B={x|x≤0或x≥4}，则B?A，
故选：B．
点评：本题考查子集的定义，以及一元二次不等式的解法，属于基础题．
练习册系列答案
阅读快车系列答案
相关题目
已知等比数列{an}各项都为正数，并且有a2•a9=4，则log2a1+log2a2+…+log2a10的值为（ ）
| A、10 | B、20 | C、30 | D、40 |
在等差数列{an}中，若S4=1，S8=4，则a17+a18+a19+a20的值为（ ）
| A、9 | B、12 | C、16 | D、17 |
函数f（x）=e
的定义域是（ ）
| x2-1 |
| A、[-1，1] |
| B、[1，+∞） |
| C、（-∞，-1] |
| D、（-∞，-1]∪[1，+∞） |
定义一种运算（a，b）*（c，d）=ac+bd，若函数f（x）=（1，log5x）*（（
）x，log2
），x0是方程f（x）=0的解，且x1＞x0，则f（x1）的值（ ）
| 1 |
| 3 |
| 1 |
| 2 |
| A、恒为正值 | B、等于零 |
| C、恒为负值 | D、不小于0 |
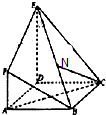如图，多面体EFABCD中，底面ABCD是正方形，AF⊥平面ABCD，DF∥AF，AB=DE=2，AF=1．