题目内容
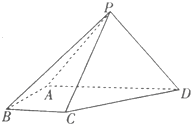 如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=
如图,在四棱锥P-ABCD中,BA⊥侧面PAD,侧棱PA=PD=| 2 |
(1)求PC与平面ABCD所成的角;
(2)求三棱锥A-PCD的体积.
考点:直线与平面所成的角,棱柱、棱锥、棱台的体积
专题:空间位置关系与距离
分析:(1)由已知得PO⊥AD,从而PO⊥平面ABCD,∠PCO是PC与平面ABCD所成的角,由此能求出PC与平面ABCD所成的角为45°.
(2)由VA-PCD=VP-ACD,利用等积法能求出三棱锥A-PCD的体积
(2)由VA-PCD=VP-ACD,利用等积法能求出三棱锥A-PCD的体积
解答:
解:(1)在△PAD中PA=PD,O为AD中点,∴PO⊥AD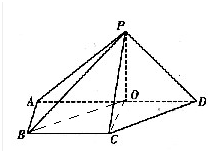
又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD
∵PO?平面PAD,∴PO⊥平面ABCD,
∴∠PCO是PC与平面ABCD所成的角,
连接BO,CO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,∴四边形OBCD是平行四边形,
∴OB∥DC.
∵AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,
∴OC=1,OB=
,
在Rt△POA中,∵AP=
,AO=1,∴OP=1,
∴∠PCO=45°,
∴PC与平面ABCD所成的角为45°.
(2)∵PO⊥平面ACD,PO=1,
S△ACD=
×AB×AD=
×1×2=1,
∴三棱锥A-PCD的体积VA-PCD=VP-ACD=
×S△ACD×PO=
×1×1=
.

又侧面PAD⊥底面ABCD,平面PAD∩平面ABCD=AD
∵PO?平面PAD,∴PO⊥平面ABCD,
∴∠PCO是PC与平面ABCD所成的角,
连接BO,CO,在直角梯形ABCD中,BC∥AD,AD=2AB=2BC,
有OD∥BC且OD=BC,∴四边形OBCD是平行四边形,
∴OB∥DC.
∵AD=2AB=2BC=2,在Rt△AOB中,AB=1,AO=1,
∴OC=1,OB=
| 2 |
在Rt△POA中,∵AP=
| 2 |
∴∠PCO=45°,
∴PC与平面ABCD所成的角为45°.
(2)∵PO⊥平面ACD,PO=1,
S△ACD=
| 1 |
| 2 |
| 1 |
| 2 |
∴三棱锥A-PCD的体积VA-PCD=VP-ACD=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
点评:本题考查线线垂直、线面垂直、线面角等基础知识,考查空间想象能力、运算求解能力、推理论证能力和探究能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在等差数列{an}中,若S4=1,S8=4,则a17+a18+a19+a20的值为( )
| A、9 | B、12 | C、16 | D、17 |
中心在原点,焦点在坐标轴上,离心率为
,且过点(2,0)的椭圆方程是( )
| ||
| 2 |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
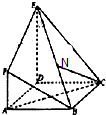 如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.
如图,多面体EFABCD中,底面ABCD是正方形,AF⊥平面ABCD,DF∥AF,AB=DE=2,AF=1.