题目内容
已知函数f(x)=
,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是( )
|
| A、(16,21) |
| B、(16,24) |
| C、(17,21) |
| D、(18,24) |
考点:对数函数图象与性质的综合应用
专题:数形结合,函数的性质及应用
分析:根据图象可判断:
<a<1,1<b<2,2<c<4,6<d<8,
当直线y=t,0<t<4,可以有4个交点,通过图象运动可以判断1×1×4×6=24,
×2×2×8=16,直线越往上走abcd的积越小,越往下abcd的积越大,即可求出答案.
| 1 |
| 2 |
当直线y=t,0<t<4,可以有4个交点,通过图象运动可以判断1×1×4×6=24,
| 1 |
| 2 |
解答:
解:若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0
根据图象可判断:
<a<1,1<b<2,2<c<4,6<d<8,
当直线y=t,0<t<4,可以有4个交点,把直线向上平移,向下平移,可判断:直线越往上走abcd的积越小,越往下abcd的积越大,
当t=0时1×1×4×6=24,当t=4时,
×2×2×8=16,abcd的取值范围是(16,24),
故选:B

根据图象可判断:
| 1 |
| 2 |
当直线y=t,0<t<4,可以有4个交点,把直线向上平移,向下平移,可判断:直线越往上走abcd的积越小,越往下abcd的积越大,
当t=0时1×1×4×6=24,当t=4时,
| 1 |
| 2 |
故选:B

点评:本题综合考查了函数图象的运用,求解两个图象的交点问题,运用动的观点解决,理解好题意是解题关键.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
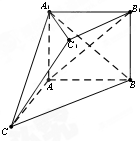 如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是
如图,在多面体ABC-A1B1C1中,四边形ABB1A1是正方形,AC=AB=1,△A1BC是 如图,平面α∥β∥γ,直线l、m分别与α、β、γ相交于点A、B、C和点D、E、F.若
如图,平面α∥β∥γ,直线l、m分别与α、β、γ相交于点A、B、C和点D、E、F.若