题目内容
已知函数y=b+ax2+2x(a、b是常数且a>0,a≠1)在区间[-
,0]上有ymax=3,ymin=
,(1)试求a和b的值.
(2)又已知函数f(x)=lg(ax2+2x+1)
①若f(x)的定义域是R,求实数a的取值范围及f(x)的值域;
②若f(x)的值域是R,求实数a的取值范围及f(x)的定义域.
| 3 |
| 2 |
| 5 |
| 2 |
(2)又已知函数f(x)=lg(ax2+2x+1)
①若f(x)的定义域是R,求实数a的取值范围及f(x)的值域;
②若f(x)的值域是R,求实数a的取值范围及f(x)的定义域.
考点:指数函数综合题
专题:函数的性质及应用,导数的综合应用
分析:(1)求y′=(2x+2)ax2+2xlna,所以讨论a>1和0<a<1两种情况,然后对每种情况求y的最大值,最小值:通过导数先找出函数y的极值,再比较两个端点的值,从而得到函数y的最大值和最小值,这样即可建立关于a,b的方程,解方程即得a,b;
(2)①f(x)的定义域为R,即ax2+2x+1>0的解集为R,所以
,这样即可求出a的取值范围.根据ax2+2x+1的值域即可求f(x)的值域;
②若f(x)的值域为R,则ax2+2x+1的值域包含(0,+∞),所以a=0时容易判断符合条件;a≠0,则需满足:
,这样即可求出a的取值范围.对应f(x)的定义域,解出不等式ax2+2x+1>0即可.
(2)①f(x)的定义域为R,即ax2+2x+1>0的解集为R,所以
|
②若f(x)的值域为R,则ax2+2x+1的值域包含(0,+∞),所以a=0时容易判断符合条件;a≠0,则需满足:
|
解答:
解:(1)y′=(2x+2)ax2+2xlna;
∴①若a>1,x∈[-
,-1)时,y′<0,x∈(-1,0)时,y′>0;
∴x=-1时,函数y取得极小值,即最小值b+
=
①;
y=b+ax2+2x=b+a(x+1)2-1;
显然,(-
+1)2-1<(0+1)2-1,又a>1;
∴x=0时,函数y取得极大值,即最大值b+1=3,b=2,带入①即可求出a=2,符合a>1;
②由①得:
x=-1时,函数y取得最大值b+
=3 ①;
x=0时,函数y取得最小值b+1=
,b=
,带入①得a=
,符合0<a<1;
所以a=2,b=2,或a=
,b=
;
(2)①因为f(x)的定义域为R,所以ax2+2x+1>0对一切x∈R成立;
由此得
解得a>1.又因为ax2+2x+1=a(x+
)2+1-
≥1-
;
∴f(x)=lg(ax2+2x+1)≥lg(1-
);
∴实数a的取值范围是(1,+∞),f(x)的值域是[lg(1-
),+∞);
②因为f(x)的值域是R,所以u=ax2+2x+1的值域包含(0,+∞);
当a=0时,u=2x+1的值域为R?(0,+∞);
当a≠0时,u=ax2+2x+1的值域包含(0,+∞),则
;
解之得0<a≤1;
∴a的取值范围是[0,1];
要使函数f(x)有意义,则:ax2+2x+1>0 ①;
由上面知方程ax2+2x+1=0有两个实根:x1=
,x2=
;
所以不等式①的解是(-∞,x1)∪(x2,+∞),即函数f(x)的定义域为(-∞,x1)∪(x2,+∞).
∴①若a>1,x∈[-
| 3 |
| 2 |
∴x=-1时,函数y取得极小值,即最小值b+
| 1 |
| a |
| 5 |
| 2 |
y=b+ax2+2x=b+a(x+1)2-1;
显然,(-
| 3 |
| 2 |
∴x=0时,函数y取得极大值,即最大值b+1=3,b=2,带入①即可求出a=2,符合a>1;
②由①得:
x=-1时,函数y取得最大值b+
| 1 |
| a |
x=0时,函数y取得最小值b+1=
| 5 |
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
所以a=2,b=2,或a=
| 2 |
| 3 |
| 3 |
| 2 |
(2)①因为f(x)的定义域为R,所以ax2+2x+1>0对一切x∈R成立;
由此得
|
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
∴f(x)=lg(ax2+2x+1)≥lg(1-
| 1 |
| a |
∴实数a的取值范围是(1,+∞),f(x)的值域是[lg(1-
| 1 |
| a |
②因为f(x)的值域是R,所以u=ax2+2x+1的值域包含(0,+∞);
当a=0时,u=2x+1的值域为R?(0,+∞);
当a≠0时,u=ax2+2x+1的值域包含(0,+∞),则
|
解之得0<a≤1;
∴a的取值范围是[0,1];
要使函数f(x)有意义,则:ax2+2x+1>0 ①;
由上面知方程ax2+2x+1=0有两个实根:x1=
-2-
| ||
| 2a |
-2+
| ||
| 2a |
所以不等式①的解是(-∞,x1)∪(x2,+∞),即函数f(x)的定义域为(-∞,x1)∪(x2,+∞).
点评:考查极值的概念,以及利用导数求函数最值的过程:先求函数f(x)的极值,再比较端点值,对数函数的值域,定义域,及解一元二次不等式.

练习册系列答案
相关题目
已知两集合M={x∈R|0≤x≤8},N={y∈R|0≤y≤5}.下列的对应关系中,是M到N的映射的是( )
A、f:x→y=2
| |||
B、f:x→y=
| |||
| C、f:x→y=2x-1 | |||
D、f:x→y=
|
已知全集U=R,集合A={y|y=lg(x2+10),x∈R),集合B={x||x-2|<1},则(∁UB)∩A=( )
| A、{x|0≤x<1或x>3} |
| B、{x|x=1或x≥3} |
| C、{x|x>3} |
| D、{x|1≤x≤3} |
已知函数f(x)=
,若存在实数a、b、c、d,满足f(a)=f(b)=f(c)=f(d),其中d>c>b>a>0,则abcd的取值范围是( )
|
| A、(16,21) |
| B、(16,24) |
| C、(17,21) |
| D、(18,24) |
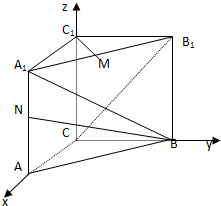 如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.
如图,直三棱柱ABC-A1B1C1的底面三角形ABC中,CA=CB=1,∠BCA=90°,棱AA1=2,M、N分别是A1B1、A1A的中点.