题目内容
如图，平面α∥β∥γ，直线l、m分别与α、β、γ相交于点A、B、C和点D、E、F．若| AB |
| BC |
| 1 |
| 3 |
考点：直线与平面平行的判定
专题：空间位置关系与距离,立体几何
分析：分两种情况：（1）直线l和m在同一平面内（2）直线l和m不在同一平面内，即l和m异面然后利用面面平行的性质定理得到线线平行，进一步利用平行线分线段成比例定理得到结果．
解答：
解：分两种情况：（1）直线l和m在同一平面内，
连结AD，BE，CF 平面α∥β∥γ，
AD∥BE∥CF，
=
=
，
DF=20，
求得：EF=15；
（2）直线l和m不在同一平面内，即l和m异面，
过D作DH∥AC，
平面α∥β∥γ，
∴AB=DG，BC=GH，
进一步得GE∥HF，
利用平行线分线段成比例得：
=
=
=
，
DF=20，
求得：EF=15，
故答案为：15．
解：分两种情况：（1）直线l和m在同一平面内，
连结AD，BE，CF 平面α∥β∥γ，
AD∥BE∥CF，
| AB |
| BC |
| DE |
| EF |
| 1 |
| 3 |
DF=20，
求得：EF=15；
（2）直线l和m不在同一平面内，即l和m异面，
过D作DH∥AC，
平面α∥β∥γ，
∴AB=DG，BC=GH，
进一步得GE∥HF，
利用平行线分线段成比例得：
| AB |
| BC |
| DG |
| GH |
| DE |
| EF |
| 1 |
| 3 |
DF=20，
求得：EF=15，
故答案为：15．
点评：本题考查的知识要点：面面平行的性质定理，直线的位置关系，平行线分线段成比例定理．
练习册系列答案
阅读快车系列答案
相关题目
已知全集U=R，集合A={y|y=lg（x2+10），x∈R），集合B={x||x-2|＜1}，则（∁UB）∩A=（ ）
| A、{x|0≤x＜1或x＞3} |
| B、{x|x=1或x≥3} |
| C、{x|x＞3} |
| D、{x|1≤x≤3} |
已知函数f（x）=
，若存在实数a、b、c、d，满足f（a）=f（b）=f（c）=f（d），其中d＞c＞b＞a＞0，则abcd的取值范围是（ ）
|
| A、（16，21） |
| B、（16，24） |
| C、（17，21） |
| D、（18，24） |
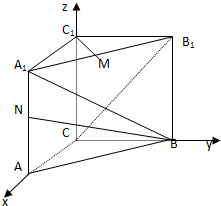如图，直三棱柱ABC-A1B1C1的底面三角形ABC中，CA=CB=1，∠BCA=90°，棱AA1=2，M、N分别是A1B1、A1A的中点．