Question

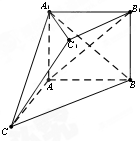如图，在多面体ABC-A₁B₁C₁中，四边形ABB₁A₁是正方形，AC=AB=1，△A₁BC是
正三角形，B₁C₁∥BC，B₁C₁=

1

2

BC．
（Ⅰ）求证：面A₁AC⊥面ABC；
（Ⅱ）求该几何体的体积．

Answer 1

考点：平面与平面垂直的判定,棱柱、棱锥、棱台的体积

专题：空间位置关系与距离

分析：（Ⅰ）由已知得A1C=A1B=

2

，A1A=AC=1，从而A₁A⊥AC，由此能证明面A₁AC⊥面ABC．
（Ⅱ）依题意得：V=VC-A1B1BA+VC-A1B1C1而VC-A1B1BA=

1

3

×SA1B1BA×CA=

1

3

×1×1=

1

3

，VC-A1B1C1=

1

3

×SA1B1C1×A1A=

1

3

×(

1

2

×

2

2

×

2

2

)×1=

1

12

，由此能求出该几何体的体积．

解答： （Ⅰ）证明：∵在多面体ABC-A₁B₁C₁中，四边形ABB₁A₁是正方形，AC=AB=1，
△A₁BC是正三角形，B₁C₁∥BC，B₁C₁=

1

2

BC，
∴A1C=A1B=

2

，A1A=AC=1，
∴A1A2+AC2=A1C2，
∴A₁A⊥AC，
又A₁A⊥AB，∴A₁A⊥平面ABC，
∴面A₁AC⊥面ABC．
（Ⅱ）解：依题意得：V=VC-A1B1BA+VC-A1B1C1
而VC-A1B1BA=

1

3

×SA1B1BA×CA=

1

3

×1×1=

1

3

，
VC-A1B1C1=

1

3

×SA1B1C1×A1A=

1

3

×(

1

2

×

2

2

×

2

2

)×1=

1

12

，
故：V=

1

3

+

1

12

=

5

12

．

点评：本题考查面面垂直的证明，考查几何体的体积的求法，解题时要认真审题，注意空间思维能力的培养．