题目内容
若三棱锥的三个侧面两两垂直，且侧棱长均为
，则其外接球的表面积为（ ）
| 3 |
| A、18π | ||
| B、36π | ||
| C、9π | ||
D、
|
考点：球的体积和表面积
专题：计算题,空间位置关系与距离
分析：根据题意可得三棱锥的三条侧棱两两垂直，因此以三条侧棱为长、宽、高构造正方体如图所示，该正方体的外接球就是三棱锥的外接球，利用长方体的对角线长公式算出球的直径，再根据球的表面积公式加以计算，可得答案．
解答：
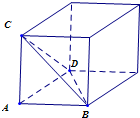解：设三棱锥A-BCD中，面ABC、面ABD、面ACD两两互相垂直，AB=AC=AD=
，
则AB、AC、AD两两互相垂直，以AB、AD、AC为长、宽、高，构造正方体如图所示，
可得该正方体的外接球就是三棱锥A-BCD的外接球，
设球半径为R，可得正方体的对角线长等于球直径2R，
即2R=3，解得R=
，
∴外接球的表面积是S=4πR2=4π×（
）2=9π．
故选：C．
解：设三棱锥A-BCD中，面ABC、面ABD、面ACD两两互相垂直，AB=AC=AD=| 3 |
则AB、AC、AD两两互相垂直，以AB、AD、AC为长、宽、高，构造正方体如图所示，
可得该正方体的外接球就是三棱锥A-BCD的外接球，
设球半径为R，可得正方体的对角线长等于球直径2R，
即2R=3，解得R=
| 3 |
| 2 |
∴外接球的表面积是S=4πR2=4π×（
| 3 |
| 2 |
故选：C．
点评：本题给出特殊的三棱锥，求它的外接球的表面积．着重考查了多面体的外接球、长方体的对角线长公式和球的表面积计算等知识，属于基础题．
练习册系列答案
黎明文化寒假作业系列答案
相关题目
小波以游戏方式决定是去打球，唱歌还是去下棋，游戏规则为以O为顶点，再从A1，A2，A3，A4，A5，A6（如图）这6个点中任取不同的两点得到∠Ai0Aj（0°＜∠AiOAj≤180°）i，j∈{1，2，3，4，5，6}若∠AiOAj为钝角或平角就去打球，若∠AiOAj为直角就去唱歌，若∠AiOAj为锐角就去下棋，则小波去打球的概率为若把一个正方形用斜二测画法画出，有下列说法：
①所得图形一定是矩形；
②所得图形一定是平行四边形；
③所得图形一定是梯形；
④原正方形的中心一定是所得图形对角线的交点．
其中正确的是（ ）
①所得图形一定是矩形；
②所得图形一定是平行四边形；
③所得图形一定是梯形；
④原正方形的中心一定是所得图形对角线的交点．
其中正确的是（ ）
| A、①②③④ | B、②④ |
| C、③④ | D、②③④ |
f（x）=
sin2x是（ ）
| 1 |
| 2 |
| A、最小正周期为2π的偶函数 |
| B、最小正周期为2π的奇函数 |
| C、最小正周期为π的偶函数 |
| D、最小正周期为π的奇函数 |