题目内容

已知数列{an}是公差不为零的等差数列，且a2=3，a4，a5，a8成等比数列．
（1）求数列{an}的通项公式．
（2）设Sn为数列{an}的前n项和，求Sn的最值．
考点：等比数列的性质
专题：综合题,等差数列与等比数列
分析：（1）由已知条件，利用等差数列的通项公式和等比数列的性质，列出方程组，求出等差数列的首项和公差，由此能求出数列{an}的通项公式．
（2）根据数列{an}的前n项和公式，即可求Sn的最值．
解答： 解：（1）设等差数列{an}的公差为d，d≠0，
∵a2=3，a4，a5，a8成等比数列，
∴
a1+d=3
(3+3d)2=(3+2d)(3+6d)
，
∵d≠0，∴解得a1=5，d=-2，
∴an=5-2（n-1）=-2n+7；
（2）Sn=
n(5-2n+7)
2
=-n2+6n=-（n-3）2+9，
∴n=3时，Sn的最大值为9．
点评：本题考查数列的通项公式和前n项和公式的求法，是中档题，
练习册系列答案
相关题目
已知x∈[-
π
12
，
π
3
]，则函数y=sin4x-cos4x的最小值是（　　）
A、-1
B、-
3
2
C、
1
2
D、1
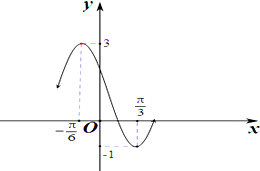已知函数g（x）=Acos（ωx+φ）+B（A＞0，ω＞0，|φ|＜
π
2
）的部分图象如图所示．
（1）将函数g（x）的图象保持纵坐标不变，横坐标向右平移
π
3
个单位后得到函数f（x）的图象，求函数f（x）在x∈[-
π
6
，
π
3
]上的值域；
（2）求使f（x）≥2的x的取值范围的集合．
已知函数f（x）=a（x2+1）+lnx．
（1）讨论函数f（x）的单调性；
（2）若对任意a∈（-4，-2）及x∈[1，3]时，恒有ma-f（x）＞a2成立，求实数m的取值范围．
已知a∈R，函数f（x）=2x2（x-a）．
（1）求函数f（x）在区间[1，2]上最小值h（a）；
（2）对（1）中的h（a），若关于a的方程h（a）=k（a+1）有两个不同的实数解，求实数k的取值范围；
（3）若点A（a1，h（a1）），B（a2，h（a2）），C（a3，h（a3）），从左到右依次是函数y=h（a）图象上三点，且这三点不共线，求证：△ABC是钝角三角形．
已知向量
a
=（cos
3
2
x，sin
3
2
x），
b
=（cos
x
2
，-sin
x
2
），且x∈[0，
π
2
]．
（1）求
a
•
b
及|
a
+
b
|
（2）若f（x）=
a
•
b
-2λ|
a
+
b
|的最小值是-
3
2
，求实数λ的值；
（3）设g（x）=sin（x+
π
3
），若方程3[g（x）]2-g（x）+m=0在x∈（-
π
3
，
2π
3
）内有两个不同的解，求实数m的取值范围．
已知函数g（x）=
2
x
+lnx，f（x）=mx-
m-2
x
-lnx，m∈R．
（1）求函数g（x）的极值点；
（2）若f（x）-g（x）在[1，+∞）上为单调函数，求m的取值范围；
（3）设h（x）=
2e
x
，若在[1，e]上至少存在一个x0，使得f（x0）-g（x0）＞h（x0）成立，求m的取值范围．
已知函数f（x）=cos2x-cosx+b，x∈R．
（1）若f（
π
2
）=1，求函数f（x）的解析式；
（2）若x∈[0，
π
3
]时，f（x）的图象与x轴有交点，求实数b的取值范围．
设全集是实数集R，A={x|2x2-7x+3≤0}，B={x|x2+a＜0}．
（1）当a=-4时，求A∩B和A∪B；
（2）若A∩B=∅，求实数a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网