题目内容
已知函数f(x)=cos2x-cosx+b,x∈R.
(1)若f(
)=1,求函数f(x)的解析式;
(2)若x∈[0,
]时,f(x)的图象与x轴有交点,求实数b的取值范围.
(1)若f(
| π |
| 2 |
(2)若x∈[0,
| π |
| 3 |
考点:三角函数中的恒等变换应用
专题:三角函数的图像与性质
分析:(1)利用f(
)=1和函数解析式求得b.
(2)利用配方法对函数解析式整理,根据x的范围,确定cosx的范围,进而二次函数的性质建立不等式组求得b的范围.
| π |
| 2 |
(2)利用配方法对函数解析式整理,根据x的范围,确定cosx的范围,进而二次函数的性质建立不等式组求得b的范围.
解答:
解:(1)f(
)=cos2
-cos
+b=1,求得b=1.
(2)由知f(x)=cos2
-cos
+b
=(cosx-
)2+b-
,
∵x∈[0,
],
∴
≤cosx≤1,
要使f(x)的图象与x轴有交点,需
,
解得0≤b≤
.
| π |
| 2 |
| π |
| 2 |
| π |
| 2 |
(2)由知f(x)=cos2
| π |
| 2 |
| π |
| 2 |
=(cosx-
| 1 |
| 2 |
| 1 |
| 4 |
∵x∈[0,
| π |
| 3 |
∴
| 1 |
| 2 |
要使f(x)的图象与x轴有交点,需
|
解得0≤b≤
| 1 |
| 4 |
点评:本题主要考查了二次函数的性质,解不等式.考查了学生基础知识的综合运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
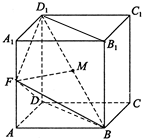 如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点.
如图,已知在棱柱ABCD-A1B1C1D1的底面是菱形,且AA1⊥面ABCD,∠DAB=60°,AD=AA1=1,F为棱AA1的中点,M为线段BD1的中点. 先后抛掷一枚骰子,得到的点数分别记为a,b,按以下程序进行运算:
先后抛掷一枚骰子,得到的点数分别记为a,b,按以下程序进行运算: